Problema
(Indicado a partir do 8º ano do E. F.)
A figura ilustra um polígono regular de [tex]9[/tex] lados. A medida do lado do polígono é [tex]a[/tex], a medida da menor diagonal é [tex]b[/tex] e a medida da maior diagonal é [tex]d[/tex].
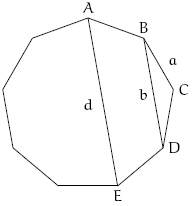
a) Determine a medida do ângulo [tex]\angle {BAE}[/tex];
b) Mostre que [tex]d=a+b[/tex].
Solução
a) Sabemos que a medida do ângulo interno do eneágono regular é igual a [tex]A_i=\dfrac{180^\circ(9-2)}{9}=140^\circ[/tex].
Considere agora o pentágono [tex]ABCDE[/tex], como indicado na figura abaixo. A soma de seus ângulos internos é [tex]540^\circ[/tex].
Como [tex]\angle{ABC}=\angle{BCD}=\angle{CDE}=140^\circ[/tex] e, pela simetria da figura, sabemos que [tex]\angle{EAB}=\angle{AED}=\alpha[/tex], então
[tex]\qquad 2\alpha+3\cdot140^\circ=540^\circ [/tex]
donde
[tex]\qquad \boxed{\alpha=60^\circ}[/tex]
b) Seja [tex]X[/tex] o ponto de intersecção das retas [tex]AB[/tex] e [tex]DE[/tex].
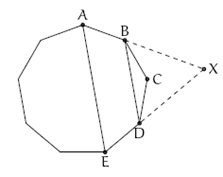
Como [tex]\angle{XAE}=\angle{XEA}=\alpha=60^\circ[/tex], o triângulo [tex]AXE[/tex] é equilátero.
O triângulo [tex]BXD[/tex] também é equilátero, pois a reta [tex]AE[/tex] é paralela à reta [tex]BD[/tex]; assim, temos [tex]AX=AE \, [/tex] e [tex] \, BX=BD[/tex].
Dessa forma, [tex]AE=AX=AB+BX=AB+BD=BC+BD[/tex], ou seja, [tex]d=a+b[/tex].
Solução elaborada pelos Moderadores do Blog.
