Problema
(Indicado a partir do 2º ano do E. M.)
Uma partícula situa-se num plano dotado de um sistema de coordenadas retangulares. Sabe-se que, se esta partícula estiver num ponto qualquer [tex](x,y)[/tex], ela consegue se deslocar imediatamente e em linha reta apenas para o ponto [tex](x+1,y)[/tex] ou para o ponto [tex](x,y+1)[/tex].
Quantos são os trajetos possíveis para que a partícula partindo do ponto [tex](0,0)[/tex] atinja o ponto [tex](10,8)[/tex], tendo passado pelo ponto [tex](5,5)[/tex]?
Solução
Antes de mais nada, vale observar que o enunciado nos explica que, com relação ao sistema de coordenadas retangulares adotado, a partícula só pode se mover
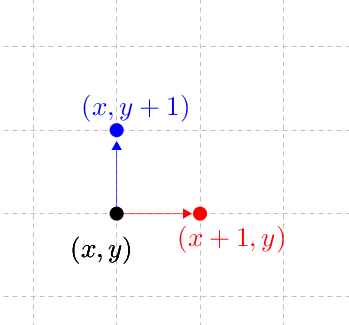
- uma unidade para a direita (quando ela se desloca de um ponto [tex](x,y)[/tex] para o ponto [tex]\textcolor{red}{(x+1,y)}[/tex]) ou
- uma unidade para cima (quando ela se desloca de um ponto [tex](x,y)[/tex] para o ponto [tex]\textcolor{blue}{(x,y+1)}[/tex]).
Para a solução, vamos analisar o problema em duas etapas:
[tex]\quad \textcolor{#800000}{(i)}[/tex] Chegar até o ponto [tex](5,5)[/tex];
[tex]\quad \textcolor{#800000}{(ii)}[/tex] Ir do ponto [tex](5,5)[/tex] ao ponto [tex](10,8)[/tex].
[tex] \textcolor{#800000}{(i)}[/tex] Para ir do ponto [tex](0,0)[/tex] ao ponto [tex](5,5)[/tex] a partícula vai ter que se deslocar cinco vezes para cima e cinco vezes para direita, só restando saber qual a ordem entre ir para direita e para cima. Isso se resume em descobrir o número de formas que se pode arrumar [tex]10[/tex] elementos, sendo [tex]5[/tex] iguais a [tex]C[/tex] e [tex]5[/tex] iguais a [tex]D[/tex]. Calculando então o número de permutações com repetição, temos [tex]\boxed{P_{10}^{5\,, \,5}=\dfrac{10!}{5! \cdot 5!_{~}}= 252}[/tex] formas de percorrer a primeira parte do trajeto.
[tex] \textcolor{#800000}{(ii)}[/tex] Agora estamos no ponto [tex](5,5)[/tex] e queremos ir ao [tex](10,8)[/tex]; então a partícula vai ter que se deslocar cinco vezes para direita e três para cima. Desta vez, vamos permutar [tex]8[/tex] elementos, sendo [tex]5[/tex] iguais [tex]D[/tex] e [tex]3[/tex] iguais a [tex]C[/tex], ou seja, temos [tex]\boxed{P_{8}^{5\,, \,3}=\dfrac{8!}{5! \cdot 3!_{~}}= 56}[/tex] formas de percorrer a segunda parte do trajeto.
Multiplicando um resultado pelo outro (Princípio Multiplicativo*), teremos o número total de possibilidades:
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$252 \times 56 = 14\;112$}[/tex] trajetos distintos.
Solução enviada pelo Clube Aprendizes dos Números , com contribuições dos Moderadores do Blog.
Participou da discussão do problema o Clube Aprendizes dos Números.

* Se você não se lembra do Princípio Multiplicativo, sugerimos que você assista a este vídeo, a este vídeo e a este .
Você pode também ler o texto “Princípio Fundamental da Contagem” na Sala de Pequenos Textos, na Nossa Biblioteca.
Bons estudos!
