.Problema de Olimpíada: Quadrado, triângulo, quadrado

Problema

---

Considere um quadrado com lado de comprimento [tex]L[/tex].
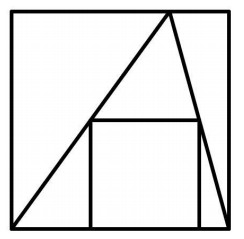
Tome um triângulo inscrito nesse quadrado e um novo quadrado inscrito no triângulo, como mostra a figura abaixo.
Determine o comprimento do lado do quadrado menor inscrito no triângulo, justificando sua resposta.

Solução

---

Considere que [tex]L[/tex] seja a medida do lado do quadrado maior [tex]ABCD[/tex] e que [tex]a[/tex] seja a medida do lado do quadrado menor [tex]FGHI[/tex], conforme mostra a figura abaixo.

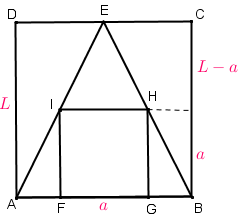
Como [tex]FGHI[/tex] é um quadrado, os lados [tex]\overline{FG}[/tex] e [tex]\overline{IH}[/tex] são paralelos; assim, os ângulos [tex]E\hat{I}H[/tex] e [tex]E\hat{A}B[/tex] são congruentes, assim como os ângulos [tex]E\hat{H}I[/tex] e [tex]E\hat{B}A[/tex]. Com isso, os triângulos [tex]EHI[/tex] e [tex]EBA[/tex] são semelhantes.
Assim, considerando que em triângulos semelhantes a razão entre os comprimentos de lados correspondentes é igual à razão entre alturas correspondentes, podemos afirmar que:

[tex]\dfrac{L}{a}=\dfrac{L}{L-a}[/tex],

ou seja,

[tex]\dfrac{L-a}{a}=\dfrac{L}{L}=1[/tex],

onde [tex]L − a \, [/tex] e [tex] \, a[/tex] são, respectivamente, os comprimentos da altura e da base do triângulo [tex]EHI[/tex]; e a base e a altura do triângulo [tex]EAB[/tex] têm comprimentos iguais a [tex]L.[/tex]
Com isso, [tex]L-a=a \, [/tex] e, finalmente, [tex]a=\dfrac{L}{2}[/tex].
Portanto, a medida do lado do quadrado menor é igual à metade da medida dada do lado do quadrado maior.

---

Solução elaborada pelos Moderadores do Blog.