Problema
Qual é o ângulo interno de menor medida em um triângulo isósceles que tem uma mediana que o divide em dois triângulos isósceles?
Solução
Seja [tex]ABC[/tex] um triângulo isósceles que tem uma mediana que o divide em dois outros triângulos isósceles.
Como [tex]ABC[/tex] tem dois lados com a mesma medida, cabe a seguinte pergunta: A mediana que divide [tex]ABC[/tex] em dois triângulos internos isósceles é relativa a um de seus lados congruentes?
Vejamos.
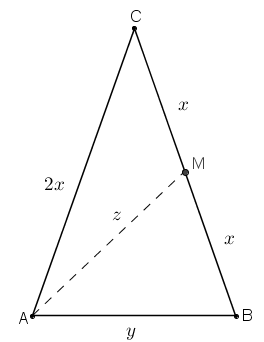 |
No triângulo [tex]ABC[/tex] ao lado, [tex]AC=BC=2x[/tex] e [tex]AB = y[/tex]. Seja [tex]\overline{AM}[/tex] a mediana relativa ao lado [tex]\overline{BC}[/tex] e suponha que os dois triângulos internos [tex]ABM[/tex] e [tex]AMC[/tex] sejam isósceles. Suponha [tex]AM=z[/tex]. Como [tex]x\ne0[/tex], [tex]x\ne 2x[/tex]; então para que [tex]AMC[/tex] seja isósceles devemos ter [tex]z=2x[/tex] ou [tex]z=x[/tex]. Mas, pela desigualdade triangular aplicada ao triângulo [tex]AMC[/tex], [tex]z+x\gt 2x [/tex], logo não podemos ter [tex]z=x[/tex]. Assim, necessariamente, [tex]z=2x[/tex]. |
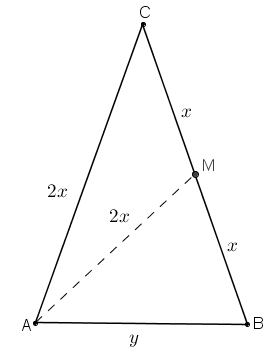 |
Mais uma vez, como [tex]x\ne 0[/tex], [tex]x\ne 2x[/tex]; então para que [tex]AMB[/tex] seja isósceles devemos ter [tex]y=2x[/tex] ou [tex]y=x[/tex]. Pela desigualdade triangular aplicada ao triângulo [tex]AMB[/tex], temos que [tex]y+x\gt 2x [/tex], logo [tex]y\ne x[/tex] e resta apenas a hipótese de que [tex]y=2x[/tex]. Mas, se [tex]y=2x[/tex], o triângulo [tex]ABC[/tex] é equilátero e, assim, a mediana [tex]\overline{AM}[/tex] seria também a altura do triângulo relativa ao lado [tex]\overline{BC}[/tex]. Com isso o triângulo [tex]AMC[/tex] seria um triângulo retângulo, o que não pode ocorrer, pois os lados [tex] 2x, \, x, \, 2x[/tex] não satisfazem o Teorema de Pitágoras, já que [tex] (2x)^2+x^2=5x^2\ne4x^2=(2x)^2[/tex]. |
Pelo exposto, a mediana que divide o triângulo [tex]ABC[/tex] em dois outros triângulos isósceles NÃO é relativa a um dos lados congruentes.
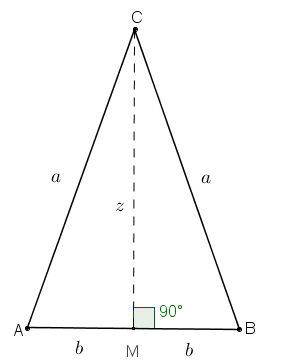 |
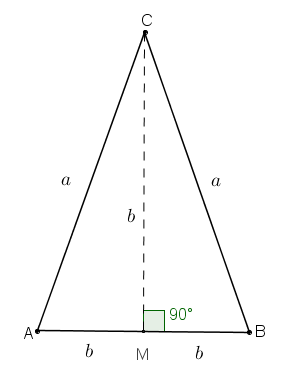
Assim, considere a mediana [tex]\overline{CM}[/tex] relativa ao lado não congruente [tex]\overline{AB}[/tex] e suponha que os triângulos [tex]ACM[/tex] e [tex]MCB[/tex] sejam isósceles. Como o próprio triângulo [tex]ABC[/tex] é isósceles, a mediana [tex]\overline{CM}[/tex] é também mediatriz, assim [tex]\widehat{M}[/tex] é um ângulo reto. Agora, se [tex]CA=CB=a \, [/tex] e [tex] \, AB=2b[/tex], qual é a medida [tex]z[/tex] da mediana [tex]CM[/tex]? Como [tex]a\gt b[/tex] e os triângulos internos são isósceles, a princípio teríamos duas possibilidades: [tex]z=a[/tex] ou [tex]z=b[/tex]. No entanto, os triângulos internos também são retângulos, logo [tex]a \gt z[/tex], assim, [tex]z\ne a[/tex] e, portanto, [tex]z=b[/tex]. |
 |
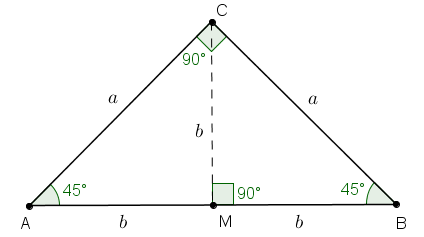
Com o triângulo [tex]ABC[/tex] determinado dentro das condições do problema, vamos responder à pergunta formulada no problema. Como os triângulos [tex]AMC[/tex] e [tex]BMC[/tex] são isósceles, cada um desses triângulos tem um par de ângulos agudos com a mesma medida. Como esses triângulos são retângulos, a soma dessas medidas é [tex]180^{\circ}-90^{\circ}=90^{\circ}[/tex] e, portanto, cada um desses triângulos tem um par de ângulos agudos, cada um medindo [tex]45^{\circ}[/tex]. Mas [tex]\widehat{A}[/tex] e [tex]\widehat{B}[/tex] são também ângulos do triângulo inicial [tex]ABC[/tex], logo, [tex]ABC[/tex] é também um triângulo retângulo isósceles. |
Portanto, a menor medida possível para um ângulo interno de um triângulo nas condições dadas é [tex]45^{\circ}[/tex].
Solução elaborada pelos Moderadores do Blog.
Aplicativos
Se você gosta de visualizar resultados geométricos, utilize os applets abaixo
para verificar, na prática, duas das situações que apareceram na solução apresentada.
Boa diversão!!
Aplicativo 1
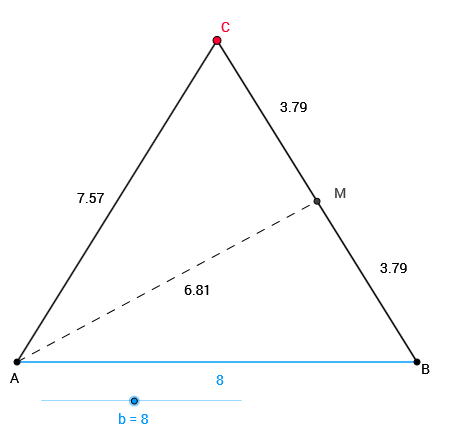
Com este applet, você pode verificar, em vários casos particulares, que a mediana relativa a um dos lados congruentes de um triângulo isósceles não divide esse triângulo em dois triângulos internos também isósceles. Para isso:
1. Clique na figura abaixo.
2. Aguarde o applet carregar. (O aplicativo vai abrir em outra janela.)
3. Escolha uma medida para a base [tex]\overline{AB}[/tex] do triângulo, movimentando horizontalmente o ponto b que aparece na parte inferior do applet.
4. Em seguida, movimente verticalmente o ponto [tex]C[/tex] para obter vários triângulos isósceles com a base [tex]\overline{AB}[/tex] fixada no passo anterior.
5. Para cada triângulo, verifique que os triângulos internos obtidos não são isósceles.
6. Quando terminar, não se esqueça de fechar a janela que se abriu.
Aplicativo 2
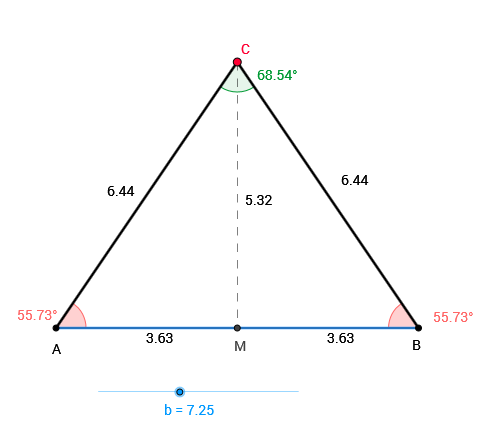
Com este segundo applet, você pode verificar, para alguns casos particulares, que se a mediana relativa ao lado não congruente de um triângulo isósceles divide esse triângulo em dois triângulos internos também isósceles, então o triângulo em questão é retângulo. Para isso:
1. Clique na figura abaixo.
2. Aguarde o applet carregar. (O aplicativo vai abrir em outra janela.)
3. Escolha uma medida para a base [tex]\overline{AB}[/tex] do triângulo, movimentando horizontalmente o ponto b que aparece na parte inferior do applet.
4. Em seguida, movimente verticalmente o ponto [tex]C[/tex] para obter vários triângulos isósceles com a base [tex]\overline{AB}[/tex] fixada no passo anterior.
5. Verifique que é possível se obter triângulos para os quais os triângulos internos obtidos são isósceles.
6. Quando o passo 5 for verificado, observe que, de fato, o triângulo isósceles [tex]ABC[/tex] obtido é retângulo.
7. Quando terminar, não se esqueça de fechar a janela que se abriu.
Nível S – 3ª série