Problema
(Indicado a partir do 1º ano do E. M.)
Para alguns números inteiros positivos [tex]p[/tex], existe um quadrilátero [tex]ABCD[/tex] tal que
- as medidas dos lados são inteiros positivos,
- o perímetro é [tex]p[/tex],
- os ângulos [tex]B[/tex] e [tex]C[/tex] são retos,
- [tex]AB=2[/tex],
- [tex]CD=AD[/tex].
Para quantos valores de [tex]p<2015[/tex] isso é possível?
Solução
Suponha um quadrilátero [tex]ABCD[/tex] que satisfaça as condições do problema. Nesse caso, sejam [tex]x[/tex] e [tex]y[/tex] inteiros positivos tais que [tex]BC = x[/tex] e [tex]CD = AD = y[/tex].
Inicialmente, considere o ponto [tex]E[/tex] de interseção da “reta que passa pelo ponto [tex]A[/tex] e é paralela ao segmento [tex]BC[/tex]” com a “reta determinada pelos pontos [tex]C[/tex] e [tex]D[/tex]”. Observe que podemos ter três situações:
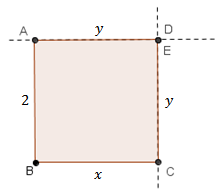
- [tex]E=D[/tex];
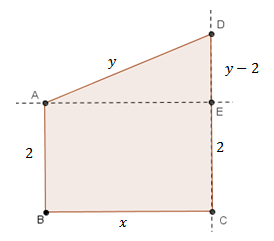
- o ponto [tex]D[/tex] está entre os pontos [tex]C[/tex] e [tex]E[/tex];
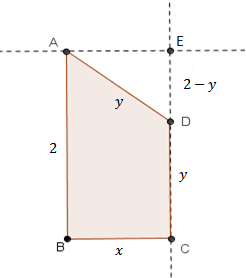
- o ponto [tex]E[/tex] está entre os pontos [tex]C[/tex] e [tex]D[/tex].
A figura abaixo ilustra as três situações.
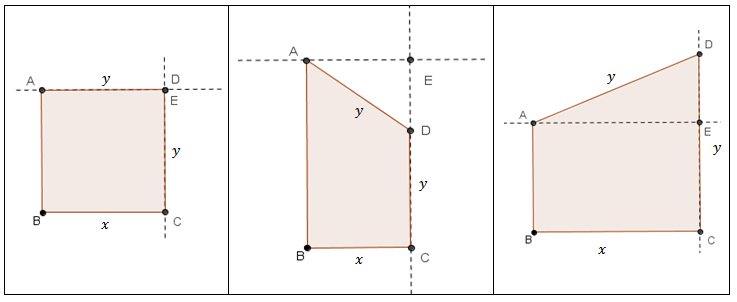
Analisemos cada uma.
|
|
(1) Como [tex]AB=2[/tex], a geometria do problema garante que [tex]x=y=2[/tex]. |
|
|
(2) Neste caso, a construção proposta garante que [tex]y\lt 2[/tex]. |
|
|
(3) Esta é a situação mais geral: [tex]y\gt 2[/tex]. Como o triângulo [tex]AED[/tex] é retângulo, aplicando o Teorema de Pitágoras obtemos [tex]x^2 + (y – 2)^2 = y^2[/tex]. Isolando [tex]y[/tex] nessa igualdade, obtemos [tex]y = \left(\dfrac{x}{2} \right)^2 + 1[/tex]. Dessa forma, o perímetro [tex]p[/tex] do quadrilátero [tex]ABCD[/tex] pode ser escrito em função de [tex]x[/tex] como |
Note que a análise geométrica da construção proposta no início desta solução mostrou três casos distintos: [tex]y= 2[/tex]; [tex]y\lt 2[/tex]; [tex]y\gt 2[/tex]. No entanto as conclusões algébricas [tex]\boxed{y = \left(\dfrac{x}{2} \right)^2 + 1} \, [/tex] e [tex] \, \boxed{p = \dfrac{x^2}{2} + x + 4}[/tex] obtidas no caso (3) fornecem, particularmente, os valores de [tex]y \, [/tex] e [tex] \, p[/tex] obtidos nos casos (1) e (2):
- se [tex]x=2[/tex], então [tex] y= 2[/tex] e [tex]p=8[/tex];
- se [tex]x=1[/tex], então [tex] y= \dfrac{5}{4}[/tex] e [tex]p=\dfrac{11}{6}[/tex].
Dessa forma, vamos continuar a solução do problema trilhando o caminho algébrico, utilizando, então, essas duas expressões para obter os valores de [tex]p[/tex] solicitados.
De [tex]y = \left(\dfrac{x}{2} \right)^2 + 1 \, [/tex] podemos concluir que [tex]x[/tex] deve ser par, já que [tex]y[/tex] é inteiro; e como o problema estabelece que [tex] p \lt 2015[/tex], então
[tex]\qquad\qquad \dfrac{x^2}{2} + x + 4 \lt 2015[/tex],
donde
[tex]\qquad\qquad \dfrac{x^2}{2} + x – 2011 \lt 0[/tex]
ou, ainda,
[tex]\qquad\qquad x^2 + 2x – 4022 \lt 0.\qquad\qquad (i)[/tex]
Considerando a função [tex]f[/tex] definida por [tex]f(x) = x^2 + 2x – 4022[/tex], podemos resolver a inequação [tex] (i)[/tex] “estudando o sinal” da função [tex]f[/tex]. Para isso, observamos que o gráfico de [tex]f[/tex] é uma parábola, com concavidade voltada para cima e que intersecta o eixo horizontal do plano cartesiano nos pontos [tex](x_1 , 0)[/tex] e [tex](x_2 , 0)[/tex], sendo [tex]x_1[/tex] e [tex]x_2[/tex] os zeros da função [tex]f[/tex] e, portanto, as raízes da equação [tex] \, x^2 + 2x – 4022=0[/tex]. (Veja figura abaixo.)

Note que:
- [tex]x[/tex] é um número inteiro par que indica o comprimento de um dos lados do quadrilátero; logo, é positivo;
- [tex]x_2 = \dfrac{-2 + \sqrt{2^2 – 4 \cdot 1 \cdot (-4022)}}{2} \approx 62,43[/tex];
assim, para resolvermos o problema, basta procurarmos os números pares do intervalo [tex]]0 , x_2[[/tex].
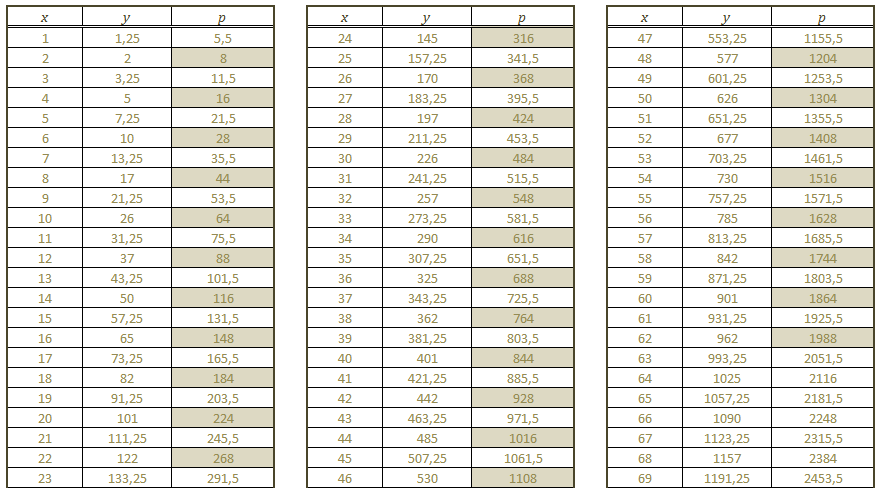
Observamos que há 31 valores possíveis para [tex]x[/tex]. Mas, para finalizarmos a solução, precisamos analisar os possíveis perímetros determinados por esses 31 valores. No entanto, isso é simples, já que o perímetro [tex]p[/tex] é dado em função de [tex]x[/tex], de modo crescente, no intervalo [tex]]0 , x_2[[/tex] (Verifique!). Portanto, os 31 valores de [tex]x[/tex] definem valores de [tex]p[/tex] distintos dois a dois.
Pelo exposto, há 31 valores possíveis de [tex]p[/tex] que satisfazem as exigências do problema.
Solução elaborada pelos Moderadores do Blog.
Aparatos
Basta movimentar o botão X do applet para obter o caso (1), o caso (2) e dois casos particulares de (3).
OBMEP_ srdg, criado com o GeoGebra
É só clicar no ícone ► que aparece no canto inferior esquerdo do applet para ver os quadriláteros correspondentes aos valores de [tex]x[/tex] de 1 a 15.
Para parar a animação, basta clicar no ícone || que aparece no canto inferior esquerdo do applet durante a animação.
Se for conveniente você pode parar a animação e mover manualmente o botão X do applet.
OBMEP_ srdg, criado com o GeoGebra
Para obter os 31 valores do perímetro que satisfazem
as condições do problema, clique no botão abaixo.