Problema
(Indicado a partir do 2º ano do E. M.)
Prove que [tex]\left( \array{ n \\ 0} \right)^2 + \left( \array{ n \\ 1} \right)^2 + \ldots + \left( \array{ n \\ n} \right)^2 = \left( \array{ 2n \\ n} \right)[/tex].
Solução
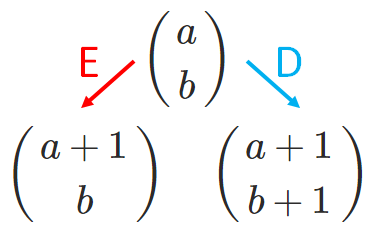 Considere o triângulo de Pascal em que podemos percorrer os números binomiais do seguinte modo:
Considere o triângulo de Pascal em que podemos percorrer os números binomiais do seguinte modo:
- estando no binomial [tex]\left(\array{a \\ b}\right)[/tex] podemos nos mover apenas para os binomiais [tex]\left(\array{a+1 \\ b}\right)[/tex] e [tex]\left(\array{a+1 \\ b+1}\right)[/tex].
Denominaremos o primeiro movimento de E e o segundo de D.
Se [tex]k[/tex] é um inteiro tal que [tex]0\lt k\le n[/tex], para sairmos do binomial [tex]\left(\array{0 \\ 0}\right)[/tex] e irmos até o [tex]\left(\array{n \\ k}\right)[/tex], cada trajeto será representado por uma sequência de [tex]k[/tex] movimentos D e [tex]n-k[/tex] movimentos E, havendo assim [tex]\left(\array{n \\ k}\right)[/tex] trajetos.
Deste modo, há [tex]\left(\array{2n \\ n}\right)[/tex] trajetos para saindo do [tex]\left(\array{0 \\ 0}\right)[/tex] chegarmos ao [tex]\left(\array{2n \\ n}\right)[/tex], e cada um desses trajetos passa exatamente por um binomial da linha [tex]n[/tex]. Podemos separar esses trajetos em grupos: os que passam pelo [tex]\left(\array{n \\ 0}\right)[/tex], os que passam pelo [tex]\left(\array{n \\ 1}\right)[/tex], … , os que passam por [tex]\left(\array{n \\ n}\right)[/tex].
A quantidade de trajetos que passam por [tex]\left(\array{n \\ k}\right)[/tex] pode ser calculada pelo princípio multiplicativo, quando dividimos esse trajeto em dois trechos: de [tex]\left(\array{0 \\ 0}\right)[/tex] a [tex]\left(\array{n \\ k}\right)[/tex] e de [tex]\left(\array{n \\ k}\right)[/tex] a [tex]\left(\array{2n \\ n}\right)[/tex].
Como já calculamos a quantidade de modos de escolhermos o primeiro trecho, passemos a quantidade de modos de escolhermos o segundo trecho. Qualquer que seja o binomial [tex]\left(\array{n \\ k}\right)[/tex], podemos recortar um subtriângulo de Pascal em que ele é o topo e [tex]\left(\array{2n \\ n}\right)[/tex] aparece na linha [tex]n[/tex] como o elemento [tex]n-k[/tex]. Desse modo, há [tex]\left(\array{n \\ n-k}\right)[/tex] modos de escolher o segundo trecho.
Assim, o número de trajetos saindo de [tex]\left(\array{0 \\ 0}\right)[/tex], passando por [tex]\left(\array{n \\ k}\right)[/tex] e chegando em [tex]\left(\array{2n \\ n}\right)[/tex] é
- [tex] \left(\array{n \\ k}\right) \cdot \left(\array{n \\ n-k}\right) = \left(\array{n \\ k}\right) \cdot \left(\array{n \\ k}\right) = \left(\array{n \\ k}\right)^2[/tex]
A soma das quantidades de trajetos de cada grupo é
- [tex]\left(\array{2n \\ n}\right)[/tex],
logo
[tex] \qquad \boxed{\left( \array{ n \\ 0} \right)^2 + \left( \array{ n \\ 1} \right)^2 + \ldots + \left( \array{ n \\ n} \right)^2 = \left( \array{ 2n \\ n} \right)}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
