Problema
(Indicado a partir do 9º ano do E. F.)
Uma lona com formato de um triângulo isósceles [tex]ABC[/tex], com [tex]AB=BC=30\,m[/tex] e [tex]AC=24\,m[/tex] , está mostrada na figura.
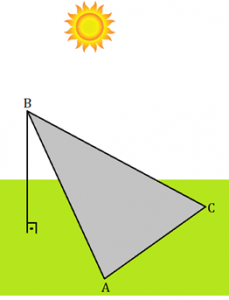
O vértice [tex]B[/tex] está a uma distância de [tex]18\,m[/tex] do chão.
Ao meio-dia, o Sol projeta no solo uma sombra dessa lona no formato de triângulo. Supondo que o Sol, neste horário, esteja exatamente “a pino”, qual a natureza desse triângulo quanto às medidas de seus lados?
Ajuda
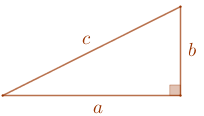
Um dos resultados mais conhecidos da Geometria é o "Teorema de Pitágoras":
Se um triângulo retângulo tem catetos com comprimentos [tex]a \, [/tex] e [tex] \, b[/tex] e hipotenusa com comprimento [tex]c[/tex], então [tex]\boxed{a^2+b^2=c^2} \, .[/tex]
Mas o que muitas pessoas não sabem é que a recíproca desse teorema também é verdadeira:
Se os lados de um triângulo medem [tex]a \, [/tex], [tex] \, b \, [/tex] e [tex] \, c \, [/tex] e [tex]\boxed{a^2+b^2=c^2} \, [/tex], então esse é um triângulo retângulo cuja hipotenusa tem comprimento [tex]c \, .[/tex]
Solução
Seja [tex]P[/tex] a projeção ortogonal de [tex]B[/tex] no solo.
Os triângulos [tex]BPC[/tex] e [tex]BPA[/tex] são retângulos, ambos de hipotenusa [tex]30\,m[/tex] e um dos catetos medindo [tex]18\,m[/tex]. Seja [tex]x[/tex] a medida do outro cateto de ambos os triângulos.
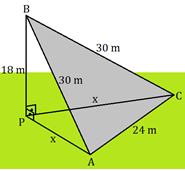
Aplicando o Teorema de Pitágoras a qualquer um dos triângulos [tex]BPC[/tex] e [tex]BPA[/tex], obtemos que [tex]x^2+18^2=30^2[/tex], donde concluímos que [tex]x=24\,m[/tex].
Assim, o triângulo [tex]PAC[/tex], que é uma projeção da tenda [tex]ABC[/tex] no solo, é equilátero de perímetro [tex]72\,m.[/tex]
Solução elaborada pelos Moderadores do Blog.
