Problema
(Indicado a partir do 1º ano do E. M.)
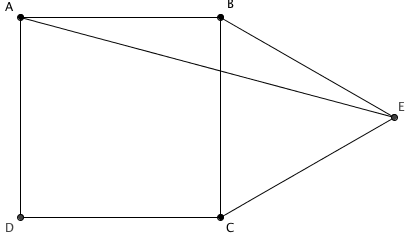
Na figura abaixo, [tex]ABCD[/tex] é um quadrado de lado [tex]a[/tex]. Construímos externamente um triângulo equilátero [tex]BCE[/tex].
Qual é a área do triângulo [tex]ABE[/tex]?
Solução
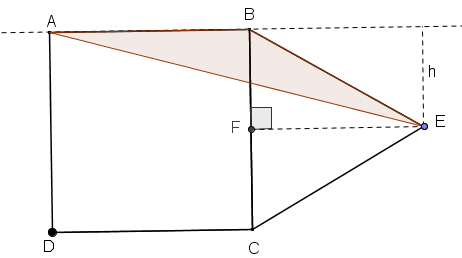
Seja [tex]F[/tex] o ponto médio de [tex]\overline{BC}[/tex].
Temos que, no triângulo equilátero [tex]BEC[/tex], [tex]\overline{EF}[/tex] é não só mediana do lado [tex]\overline{BC}[/tex], como também altura do triângulo relativa a esse lado, logo [tex]B\hat{F}E[/tex] é um ângulo reto.
Perceba também que as retas [tex]AB[/tex] e [tex]EF[/tex] são paralelas, já que a transversal [tex]BC[/tex] produz com elas ângulos alternos internos retos.
Finalmente, [tex]\overline{BF}[/tex] indica a distância entre as retas [tex]AB[/tex] e [tex]EF[/tex]; e fornecendo a distância de [tex]E[/tex] à reta [tex]AB[/tex], temos que [tex]\overline{BF}[/tex] fornece a medida da altura do triângulo [tex]ABE[/tex] relativa ao lado [tex]\overline{AB}[/tex].
Podemos, então, calcular a área [tex]S[/tex] do triângulo [tex]ABE[/tex] como se segue:
- [tex]S = \dfrac{1}{2}\cdot a \cdot \dfrac{a}{2} = \dfrac{a^2}{4}[/tex].
Solução elaborada pelos Moderadores do Blog.
Visualização da solução
Você pode utilizar este applet para construir quadrados com diferentes comprimentos de lados e, com isso, observar a veracidade da afirmação demonstrada, quantas vezes você quiser!
