Problema
(Indicado a partir do 9º ano do E. F.)
Uma ilha tem o formato de um triângulo. Supondo que essa ilha seja plana, qual é o ponto mais distante do mar?
Justifique sua resposta.
Solução
O ponto mais distante do mar é o centro do círculo inscrito no triângulo que representa a ilha. Esse ponto também é chamado incentro (o encontro das três bissetrizes de um triângulo). Vamos então denotar o centro desse círculo por [tex]O[/tex] e o raio desse círculo por [tex]r[/tex].
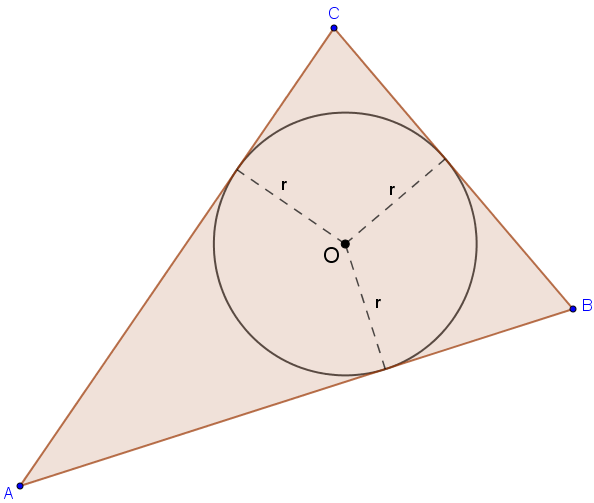
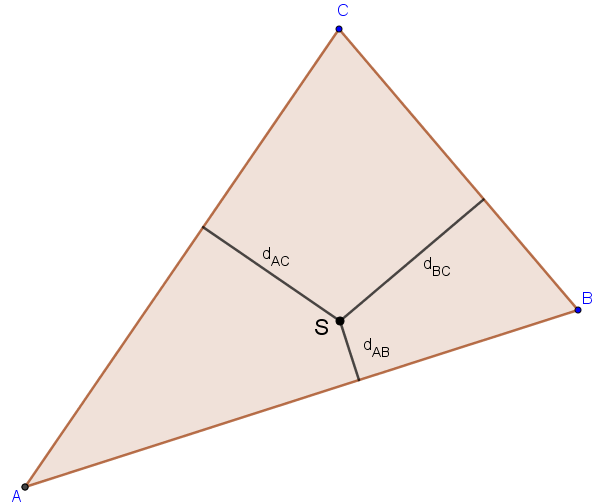
Suponhamos que seja possível determinar um ponto [tex]S[/tex] interno ao triângulo que esteja a uma distância maior dos três lados do que o ponto [tex]O[/tex].
Sejam [tex]d_{AB}[/tex], [tex]d_{BC}[/tex] e [tex]d_{AC}[/tex] as distâncias do ponto [tex]S[/tex] aos lados [tex]AB[/tex], [tex]BC[/tex] e [tex]CA[/tex], respectivamente, e [tex]|AB|[/tex], [tex]|BC|[/tex] e [tex]|CA|[/tex] os respectivos comprimentos desses lados.
Se, genericamente, [tex]P_{\Delta XYZ}[/tex] denotar a área do triângulo [tex]XYZ[/tex], observando a primeira figura temos que:
[tex]\qquad P_{\Delta ABC} = P_{\Delta AOB}+P_{\Delta BOC}+P_{\Delta AOC} \\
\qquad P_{\Delta ABC}= \dfrac{|AB| \times r + |BC| \times r + |CA| \times r }{2} \\
\qquad P_{\Delta ABC}= \dfrac{r \times (|AB| + |BC| + |CA|)}{2}. \hspace{1cm} (I)[/tex]
Observando agora a segunda figura, como assumimos que [tex]d_{AB} > r[/tex], [tex]d_{BC} > r[/tex] e [tex]d_{AC} > r[/tex], segue que:
[tex]~~ P_{\Delta ABC} = P_{\Delta ASB}+P_{\Delta BSC}+P_{\Delta ASC} =\\
~~ \dfrac{|AB| \times d_{AB} + |BC| \times d_{BC} + |CA| \times d_{AC} }{2} \gt \dfrac{|AB| \times r + |BC| \times r + |CA| \times r }{2}=\\
~~ = \dfrac{r \times (|AB| + |BC| + |CA|)}{2}[/tex]
ou seja,
[tex]~~ P_{\Delta ABC} \gt \dfrac{r \times (|AB| + |BC| + |CA|)}{2}.\hspace{1cm} (II)[/tex]
Comparando [tex](I)[/tex] e [tex](II)[/tex], temos que [tex]P_{\Delta ABC} > P_{\Delta ABC}[/tex], o que é uma contradição.
Portanto, não existe um ponto mais distante dos três lados do triângulo do que o ponto [tex]O[/tex], centro do círculo inscrito no triângulo.
Solução elaborada pelos Moderadores do Blog.
Testando a solução
Você pode utilizar este applet para simular diferentes condições iniciais para a Ilha Triangular e, com isso, observar a veracidade da afirmação demonstrada, quantas vezes você quiser!
O applet irá abrir em outra janela.
Bons estudos!
