(A) Problema para ajudar na escola: Uma enorme adição – Desafio

Problema
(A partir do 1º ano do E. M.- Nível de dificuldade: Muito Difícil)

---

(XXIX OPM, 2010) A adição

• $9 + 99 + 999 + 9999 + \cdots$

foi efetuada até o aparecimento de exatamente $9\,999$ algarismos $1$ na soma resultante.
Quantas parcelas teve essa adição?

Solução

---

O que o problema nos pede é qual o menor número natural $n$ tal que a soma
$\qquad S_n=9+99+999+\cdots+ \underbrace{99\cdots 99}_{n\text{ noves}}$
tenha exatamente $9\,999$ algarismos $1$.
Vamos reescrever a soma $S_n$ de modo que apareçam os algarismos $1$ para que possamos contá-los. Observe:
$\qquad S_n=(10-1)+(100-1)+(1000-1)+\cdots+ \big(1\underbrace{0000\cdots 00}_{n\text{ zeros}}-1\big)\\ \qquad S_n=(10^1-1)+(10^2-1)+(10^3-1)+\cdots+ (10^n-1\big)\\ \qquad S_n=\left(10^1+10^2+10^3+\cdots+10^n\right)+(\underbrace{-1-1-1-\cdots-1}_{n\text{ parcelas}})\\ \qquad S_n=\left(10^1+10^2+10^3+\cdots+10^{n-1}+10^n\right)-n\\ \qquad S_n=\underbrace{11\cdots 111}_{n\text{ uns}}0-n.\qquad \qquad \textcolor{#800000}{(i)}$
(Se você não entendeu a última passagem que fizemos, talvez a figura abaixo possa lhe ajudar!)

Observe a igualdade $\textcolor{#800000}{(i)}$ e perceba que:

• a soma $S_n$ pode ser escrita como uma diferença entre "um número com $n$ algarismos iguais a um e o último algarismo igual a zero" e "$n$".
  $\qquad S_{\textcolor{#FF00FF}{1}}=9=10-{\textcolor{#FF00FF}{1}}$
  $\qquad S_{\textcolor{#FF00FF}{2}}=108=110-{\textcolor{#FF00FF}{2}}$
  $\qquad S_{\textcolor{#FF00FF}{3}}=1107=\underbrace{111}_{{\textcolor{#FF00FF}{3}}\text{ uns}}0-{\textcolor{#FF00FF}{3}}$
  $\qquad S_{\textcolor{#FF00FF}{4}}=11106=\underbrace{1111}_{{\textcolor{#FF00FF}{4}}\text{ uns}}0-{\textcolor{#FF00FF}{4}}$
  $\qquad S_{\textcolor{#FF00FF}{5}}=111105=\underbrace{11111}_{{\textcolor{#FF00FF}{5}}\text{ uns}}0-{\textcolor{#FF00FF}{5}}$
  $\qquad S_{\textcolor{#FF00FF}{6}}=1111104=\underbrace{111111}_{{\textcolor{#FF00FF}{6}}\text{ uns}}0-{\textcolor{#FF00FF}{6}}$
  $\qquad S_{\textcolor{#FF00FF}{7}}=11111103=\underbrace{1111111}_{{\textcolor{#FF00FF}{7}}\text{ uns}}0-{\textcolor{#FF00FF}{7}}$, etc.
• para $n \gt 1$, a soma $S_n$ tem $n+1$ algarismos, já que a quantidade de dígitos do minuendo $\boxed{11\cdots 1110}$ é muito maior do que a do subtraendo $\boxed{n}$.
  $\qquad S_{\textcolor{#FF00FF}{2}}=108$; com ${\textcolor{#FF00FF}{2}}+1=3$ algarismos
  $\qquad S_{\textcolor{#FF00FF}{3}}=1107$; com ${\textcolor{#FF00FF}{3}}+1=4$ algarismos
  $\qquad S_{\textcolor{#FF00FF}{4}}=11106$; com ${\textcolor{#FF00FF}{4}}+1=5$ algarismos
  $\qquad S_{\textcolor{#FF00FF}{5}}=111105$; com ${\textcolor{#FF00FF}{5}}+1=6$ algarismos
  $\qquad S_{\textcolor{#FF00FF}{6}}=1111104$; com ${\textcolor{#FF00FF}{6}}+1=7$ algarismos
  $\qquad S_{\textcolor{#FF00FF}{7}}=11111103$; com ${\textcolor{#FF00FF}{7}}+1=8$ algarismos, etc.

Então, para termos uma soma com $9\,999$ algarismos, devemos ter $n \geqslant 9998$. Mas observe também que, por $\textcolor{#800000}{(i)}$:

• $S_{9998}=\underbrace{11\cdots 111}_{9998\text{ uns}}0-9998=\underbrace{11\cdots 11}_{9994\text{ uns}}01112\,\,$ (Veja esqueminha abaixo.);
• $S_{9999}=\underbrace{11\cdots 111}_{9999\text{ uns}}0-9999=\underbrace{11\cdots 11}_{9995\text{ uns}}01111\,\,$ (Veja esqueminha abaixo.).

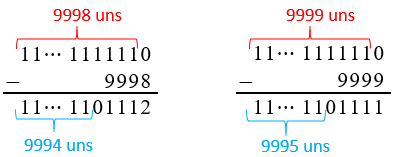
Portanto, para que a soma resultante da adição $\,\boxed{9 + 99 + 999 + 9999 + \cdots}$ tenha exatamente $9\,999$ algarismos $1$, serão necessárias $\;\fcolorbox{black}{#eee0e5}{$9\,999 \text{ parcelas}$}\,.$

---

Solução elaborada pelos Moderadores do Blog.