(A) Problema para ajudar na escola: É um paralelogramo?

Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Fácil)

---

Os pontos [tex]A,B,C[/tex] e [tex]D[/tex], quando representados em um mesmo sistema cartesiano [tex]xOy[/tex], têm como coordenadas:

• [tex]A=\left(0,0\right) [/tex] ;
• [tex]B=\left(2,7\right) [/tex] ;
• [tex]C=\left(0,4\right) [/tex] ;
• [tex]D=\left(2,3\right).[/tex]

Verifique se esses quatro pontos definem um paralelogramo.

Solução

---

Vamos inicialmente representar os pontos [tex]A,B,C[/tex] e [tex]D[/tex] em um mesmo sistema cartesiano [tex]xOy[/tex].
Para verificar se os pontos [tex]A,B,C[/tex] e [tex]D[/tex] definem um paralelogramo basta verificarmos se o quadrilátero [tex]ACBD[/tex] tem lados opostos paralelos ou não. (Observe que ter ângulos opostos e lados opostos congruentes é uma consequência da definição de paralelogramo e não parte dela.)

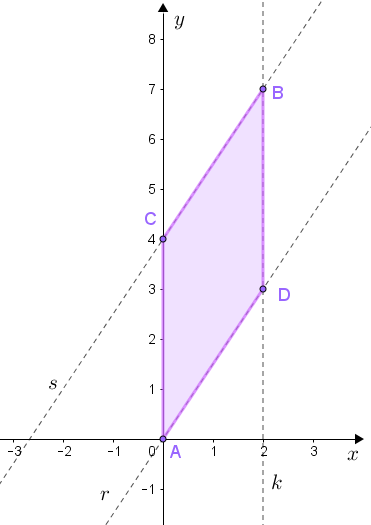
Para isso, vamos verificar se:

• a reta suporte do segmento [tex]AC[/tex] é paralela à reta suporte do segmento [tex]DB[/tex] e
• a reta suporte do segmento [tex]AD[/tex] é paralela à reta suporte do segmento [tex]CB[/tex].

Lembrando que duas retas distintas traçadas em um mesmo plano cartesiano são paralelas se, e somente se, " ambas forem verticais " ou " não sendo verticais, tiverem coeficientes angulares iguais ", observe que:

[tex]\textcolor{#800000}{(i)}[/tex] Como os pontos [tex]B[/tex] e [tex]D[/tex] têm a mesma abcissa ([tex]x_B=x_D=2[/tex]); então a distância desses pontos ao eixo vertical [tex]Oy[/tex] é a mesma. Logo, a reta [tex]k[/tex] é paralela ao eixo [tex]Oy[/tex] e, consequentemente, os segmentos [tex]AC[/tex] e [tex]DB[/tex] são paralelos.

[tex]\textcolor{#800000}{(ii)}[/tex] Como as retas [tex]r[/tex] e [tex]s[/tex] não são verticais, vamos calcular seus respectivos coeficientes angulares [tex]m_r[/tex] e [tex]m_s[/tex]



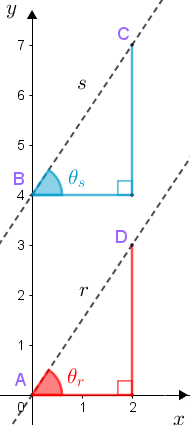
[tex]\qquad m_r=tg \, \theta_r=\dfrac{3}{2}[/tex];

[tex]\qquad m_s=tg \, \theta_s=\dfrac{7-4}{2}=\dfrac{3}{2}.[/tex]

Dessa forma, podemos concluir que os segmentos [tex]AD[/tex] e [tex]BC[/tex] são também paralelos.

Por[tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], segue que os pontos [tex]A,B,C[/tex] e [tex]D[/tex] definem um paralelogramo.

---

Solução elaborada pelos Moderadores do Blog.