Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Utilizando três semicircunferências, dividimos um círculo de raio [tex]6\, cm[/tex] em três regiões idênticas, as quais foram coloridas conforme mostra a figura.

– Qual é a área de cada região colorida? Expresse o resultado em [tex] cm^2[/tex] e em [tex] m^2[/tex].
– Qual é o perímetro de cada região colorida? Expresse o resultado em [tex] cm[/tex] e em [tex] m[/tex].

Lembrete
Como o raio do círculo foi dado em centímetros, vamos obter, inicialmente, a área e o perímetro solicitados no problema em [tex] cm^2[/tex] e [tex] cm\, [/tex], respectivamente. Assim, para finalizarmos a solução, será necessário converter a área e o perímetro obtidos para [tex]m^2\, [/tex] e [tex]m\, .[/tex]
Os esqueminhas abaixo podem ajudar!
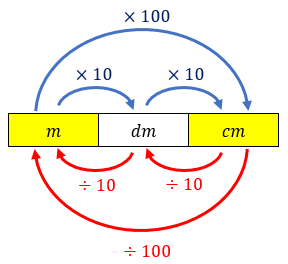 [tex]\qquad \qquad [/tex]
[tex]\qquad \qquad [/tex]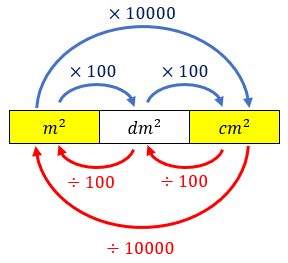
Solução
- Como o círculo foi dividido em três regiões idênticas, a área de cada região colorida é um terço da área do círculo original.
Assim, se a área de cada uma dessas regiões coloridas for denotada por [tex]A\, [/tex], então:[tex]\qquad A=\dfrac{\pi \times r^2}{3}[/tex]
[tex]\qquad A=\dfrac{\pi \times 6^2}{3}[/tex]
[tex]\qquad A=\dfrac{36\pi}{3}[/tex]
[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$A=12\pi\, cm^2$}[/tex][tex]\qquad \, \fcolorbox{black}{#eee0e5}{$A=\dfrac{12\pi}{10000}\, m^2=0,0012\pi\, m^2$}\, .[/tex]
- Observar e analisar o círculo dividido pelas três circunferências antes de as três regiões serem coloridas pode ajudar a encontrar o perímetro de cada uma delas.
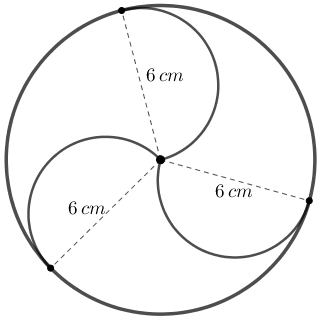
Veja que cada região é limitada por duas semicircunferências de diâmetro [tex]6\, cm[/tex] e por um terço do arco da circunferência que define o círculo original. Dessa forma, se [tex]P\, [/tex] é o perímetro de uma das regiões coloridas, então:
[tex]\qquad P=2\times \dfrac{2\times \pi \times 3}{2}+\dfrac{2\times \pi \times 6}{3}[/tex]
[tex]\qquad P=6\pi+4\pi[/tex]
[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$P=10\pi\, cm$}[/tex]
[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$P=\dfrac{10\pi}{100}\, m=0,1\pi\, m$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
