Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
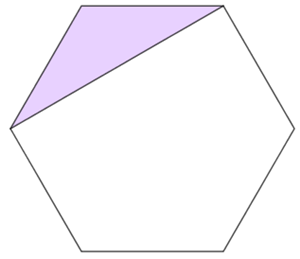
Na figura, vemos um hexágono regular cuja área é [tex] 36 \, \text{m}^2[/tex].
Qual é a área do triângulo colorido?
Expresse essa área em [tex] \text{cm}^2[/tex] e em [tex]\text{m}^2[/tex].
Solução
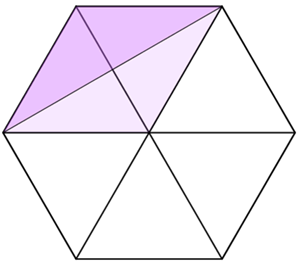
- A partir do seu centro, um hexágono regular pode ser decomposto em seis triângulos equiláteros congruentes cujo comprimento dos lados é o comprimento dos lados do próprio hexágono.
OBMEP_srdg, criado com o GeoGebra
- Observe, agora, que o triângulo colorido da figura dada no problema corresponde à metade do paralelogramo definido por dois dos seis triângulos equiláteros que decompõem o hexágono original.
Dessa forma, a área [tex]A[/tex] do triângulo colorido pode ser assim calculada:
[tex]\qquad A=\dfrac{\text{Área do paralelogramo}}{2}[/tex]
[tex]\qquad A=\dfrac{2 \times \text{Área do triângulo equilátero}}{2}[/tex]
[tex]\qquad A=\dfrac{\cancel{2} \times \text{Área do triângulo equilátero}}{\cancel{2}}[/tex]
[tex]\qquad A= \text{Área do triângulo equilátero}[/tex]
[tex]\qquad A=\dfrac{\text{Área do hexágono}}{6}[/tex]
[tex]\qquad A=\dfrac{36}{6}[/tex]
e, portanto, a área do triângulo colorido é [tex]\, \fcolorbox{black}{#edd2ff}{$6\, \text{m}^2$}\, .[/tex]
Para finalizarmos a solução do problema, precisamos converter [tex]6\, \text{m}^2\, [/tex] em [tex]\text{cm}^2\, .[/tex]
O esqueminha abaixo pode ajudar!
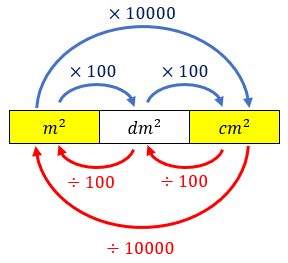
- Área do triângulo colorido em [tex]\text{cm}^2:[/tex]
[tex]\qquad 6\, \text{m}^2 \times 10000 \longmapsto\fcolorbox{black}{#edd2ff}{$60000\, \text{cm}^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
