Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
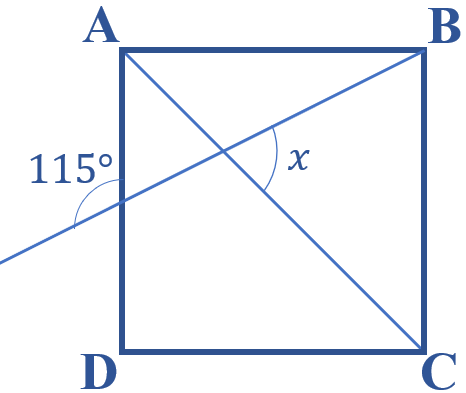
Na figura, vemos um quadrado [tex]ABCD[/tex]. Determine o valor de [tex]x[/tex], em graus.

Lembretes
(1) A medida de um ângulo externo a um triângulo qualquer é a soma das medidas dos ângulos internos do triângulo que não são adjacentes a ele.
(2) Ângulos opostos pelo vértice têm a mesma medida.
(3) Em um quadrado, as diagonais são bissetrizes dos ângulos internos.
Solução
Para facilitar a solução, consideremos os pontos [tex]E \, [/tex] e [tex] \, F[/tex], vértices dos ângulos de medidas [tex]115^{\circ} \, [/tex] e [tex]x[/tex], respectivamente, conforme ilustra a figura a seguir.
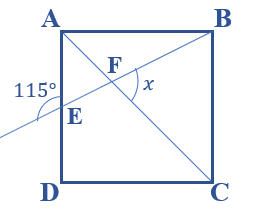
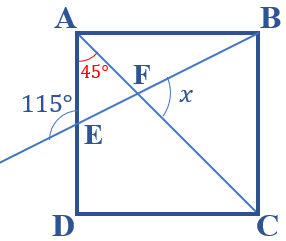
- Como [tex]\overline{AC}[/tex] é uma diagonal do quadrado [tex]ABCD[/tex], pelo Lembrete (3), [tex]\overline{AC}[/tex] divide o ângulo reto [tex]D\hat{A}B[/tex] em dois ângulos com a mesma medida. Assim, em particular, a medida do ângulo [tex]D\hat{A}C[/tex] é [tex]45^{\circ}[/tex].
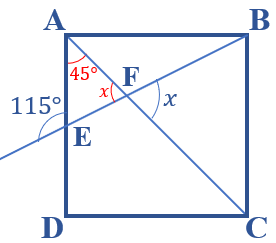
- Observe que os ângulos [tex]A\hat{F}E \, [/tex] e [tex]B\hat{F}C \, [/tex] são opostos pelo vértice. Assim, pelo Lembrete (2), a medida do ângulo [tex]A\hat{F}E \, [/tex], em graus, é [tex]x \, .[/tex]
- Finalmente, veja que o ângulo com medida [tex]115^{\circ} \, [/tex] indicado na figura é externo ao triângulo [tex]AFE \, [/tex]; logo, pelo Lembrete (1), segue que:
[tex]\qquad 115^{\circ}=x+45^{\circ}[/tex]
[tex]\qquad x=115^{\circ}-45^{\circ}[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$x=70^{\circ}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
