Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
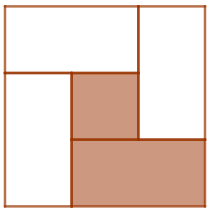
(OPM – 2011) O quadrado representado na figura tem [tex]400 \, \text{cm}^2[/tex] de área e o seu interior foi dividido em quatro retângulos que têm a mesma área e um quadradinho. A área da região colorida é [tex]112 \, \text{cm}^2[/tex].
Qual é o comprimento e a largura de cada um dos retângulos?
Solução
Como a área do quadrado grande é [tex]400 \, \text{cm}^2[/tex], então os lados desse quadrado medem [tex]20 \, \text{cm}[/tex] cada um.
Observe, agora, que a área equivalente a quatro regiões coloridas é igual à área do quadrado maior mais a área de três quadrados menores.
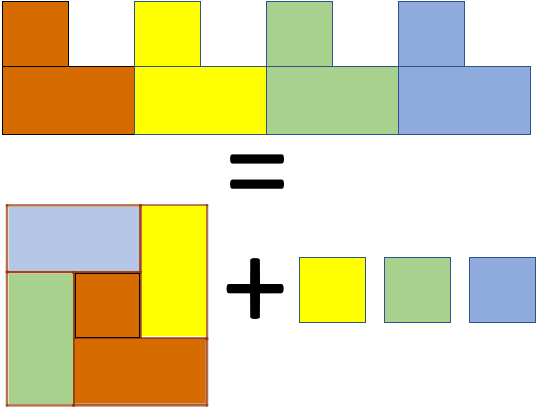
Assim, como a área do quadrado maior é [tex]A_Q=400 \, \text{cm}^2 \, [/tex], se denotarmos a área do quadrado menor por [tex]A_q \, [/tex], segue que:
[tex]\qquad 4\times 112=A_Q+3\times A_q[/tex]
[tex]\qquad 448=400+3\times A_q[/tex]
[tex]\qquad 3\times A_q=48[/tex]
[tex]\qquad A_q=16 \, \text{cm}^2[/tex]
e, com isso, os lados do quadrado menor medem [tex]\boxed{ 4 \, \text{cm}} \, .[/tex]
Perceba que:
- o comprimento de um lado do quadrado grande é igual à soma do comprimento do lado do quadrado pequeno mais duas larguras de retângulos;
assim, como os comprimentos dos lados do quadrado maior e do quadrado menor são, respectivamente, [tex]20 \, \text{cm}[/tex] e [tex]4 \, \text{cm}[/tex], segue que a largura de cada retângulo da figura é dada por [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{20-4}{2}=8 \, \text{cm}$} \, .[/tex]
Por outro lado, perceba também que
- o comprimento de um lado do quadrado grande é igual à soma de um comprimento e de uma largura dos retângulos;
portanto, podemos concluir que o comprimento de cada retângulo é dado por [tex] \, \fcolorbox{black}{#eee0e5}{$20-8=12 \, \text{cm}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
