(A) Problema para ajudar na escola: Caminho para um jardim

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)

Em uma praça, será utilizado um terreno retangular de $4 \, m$ por $8 \, m$ para se fazer um jardim.
O autor do projeto decidiu construir uma calçada pavimentada em torno da área a ser plantada, de modo que fiquem $12$ metros quadrados de terra para cultivar flores.

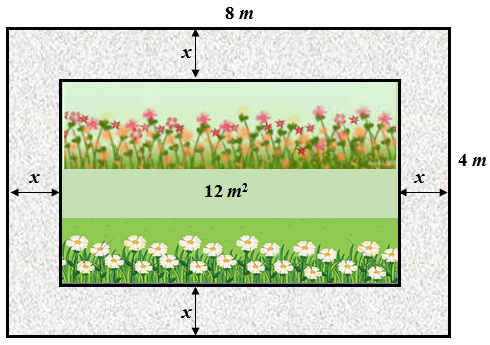
Qual deve ser a largura da calçada?

Solução

Observe que a área total de $32 \, m^2$ destinada ao jardim pode ser decomposta em cinco áreas, de acordo com a figura a seguir, na qual as medidas estão expressas em $m^2 \, .$

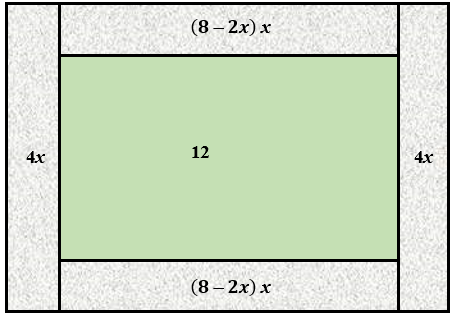
Assim, temos que:
$\qquad 32=\left(8-2x\right)\cdot x+\left(8-2x\right)\cdot x+4x+4x+12$
$\qquad 32=8x-2x^2+8x-2x^2+8x+12$
$\qquad 20=24x-4x^2$
$\qquad 4x^2-24x+20=0$
$\qquad x^2-6x+5=0 \, .\qquad \textcolor{#800000}{(i)}$
Resolvendo a equação do segundo grau $\textcolor{#800000}{(i)}$ teremos as possíveis soluções do problema. Apliquemos, então, a fórmula de resolução de uma equação do segundo grau:

$\qquad x=\dfrac{-\left(-6\right) \pm\sqrt{\left(-6\right)^2-4 \times 1 \times 5}}{2 \times 1}$

$\qquad x=\dfrac{6 \pm\sqrt{36-20}}{2}$

$\qquad x=\dfrac{6 \pm\sqrt{16}}{2}$

$\qquad x=\dfrac{\cancel{6} \pm \cancel{4}}{\cancel{2}}$

$\qquad x=3 \pm 2 \, .$

Obtemos, assim, duas raízes para a equação $\textcolor{#800000}{(i)} \,$: $x_1=5$ e $x_2=1 \,$. Mas, destas, apenas a segunda nos interessa, já que pela geometria do problema a medida $x$ não pode ser maior do que $4$.
Portanto, a largura da passarela deverá ser $\, \fcolorbox{black}{#eee0e5}{$1 \, m$} \, .$

Solução elaborada pelos Moderadores do Blog.