(A) Problemão: Dois retângulos e dois quadrados

Problema
(Indicado a partir do 9º ano do E. F.)

---

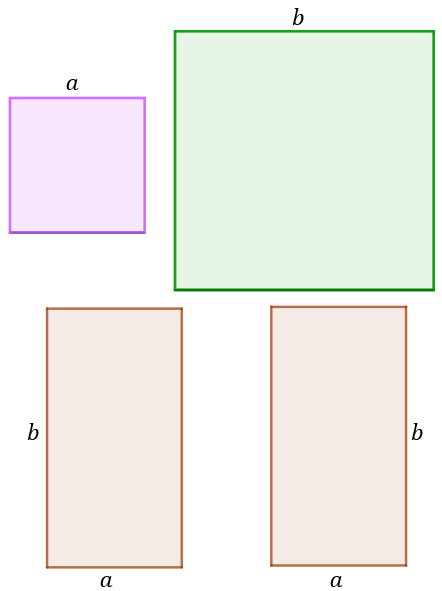
Que relações algébricas podemos deduzir a partir da imagem abaixo, na qual visualizamos dois retângulos iguais e dois quadrados não necessariamente iguais?

 

Você pode utilizar um APPLET para ajudar na solução do problema. É só clicar no botão abaixo!

Solução 1

---

– Se o comprimento do lado do quadrado menor é $a$, a sua área é dada por $a \cdot a = a^2.$
– Se o comprimento do lado do quadrado maior de $b$, a sua área é dada por $b \cdot b = b^2.$
– Os dois retângulos possuem lados medindo $a$ e $b$, logo suas áreas são dadas por $ab.$
Podemos juntar os dois quadrados e os dois retângulos para formar um único quadrado de lados $a+b$, como mostrado na figura abaixo.

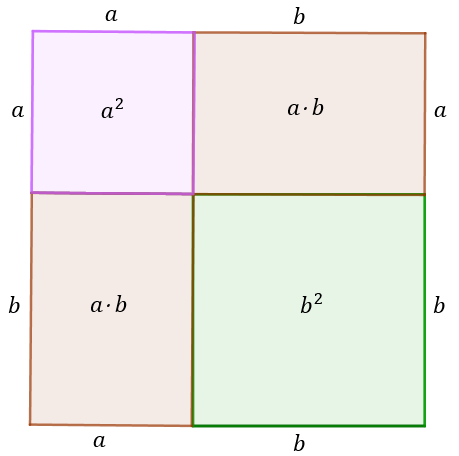
A aérea deste novo quadrado é dada por $(a+b) \cdot (a+b) = (a+b)^2$
Como formamos o quadrado de lado $(a+b)$ utilizando as figuras mostradas no enunciado, a sua área será igual a soma da área de todas elas, ou seja:
$\qquad (a+b)^2 = a^2 + b^2 + ab + ab$
$\qquad \boxed{~(a+b)^2 = a^2 + 2ab + b^2}~.$
Assim, podemos notar que acabamos de fazer uma demonstração geométrica do produto notável do quadrado de uma soma!

---

COM Potências de Euler (EECIT Lynaldo Cavalcanti de Albuquerque – Patos, PB).
Equipe COM – OBMEP.

Solução 2

---

Vamos, agora, considerar $a \gt b \gt 0$. Teremos, então um quadrado rosa maior do que o verde, mas as expressões das áreas se mantêm:
– O comprimento do lado do quadrado maior é $a$ e a sua área é $a \cdot a = a^2.$
– O comprimento do lado do quadrado menor é $b$ e a sua área é $b \cdot b = b^2.$
– Os dois retângulos possuem lados medindo $a$ e $b$ e suas áreas são $ab.$

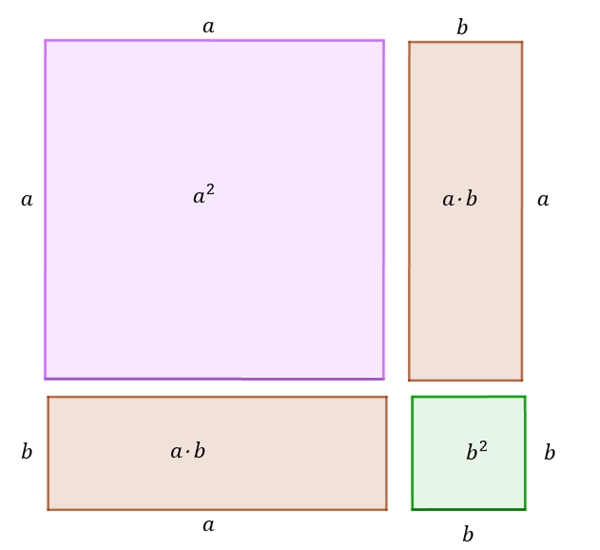
Vamos inserir os dois retângulos dentro do quadrado maior e calcular a área rosa que não ficou coberta. Observe a figura abaixo e note que essa região rosa é um quadrado de área $\left(a-b\right)^2.$

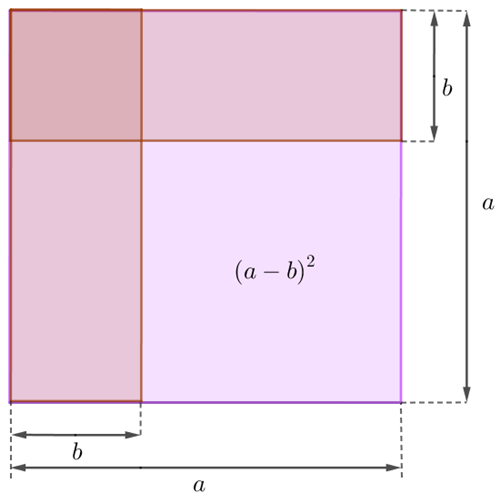
Mas como calcular essa área utilizando os dois retângulos que a definiram?
Observe que a área do quadrado de área de $(a-b)^2$ também pode ser assim calculada:
– Partimos da área total do quadrado original rosa ($a^2$).
– Retiramos duas vezes a área do retângulo ($a\cdot b$).
– Como a área correspondente ao quadradinho rosa de lado $b$ está sendo retirada duas vezes pela operação anterior, adicionamos o quadradinho verde na construção geométrica, para que as relações algébricas fiquem corretas.

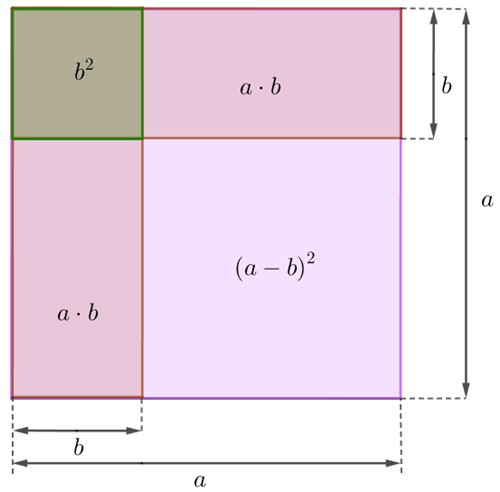
Dessa forma, segue que:
$\qquad \left(a-b\right)^2=a^2-a\cdot b-a\cdot b+b^2\\ \qquad \boxed{~\left(a-b\right)^2=a^2-2ab+b^2}~.$
O que fizemos agora foi uma demonstração geométrica do produto notável do quadrado de uma diferença!

---

COM Potências de Euler (EECIT Lynaldo Cavalcanti de Albuquerque – Patos, PB).
Equipe COM – OBMEP.