.Problemão: Dois quadrados e dois retângulos

Link do problema para dispositivos da Apple.

Problema
(Indicado a partir do 9º ano do E. F.)

Que relação algébrica é possível deduzir a partir da imagem abaixo, na qual visualizamos dois retângulos iguais, embora coloridos com cores distintas, e dois quadrados distintos?

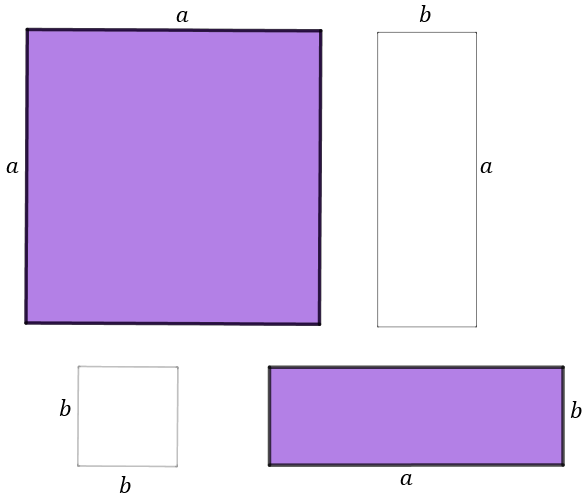
Você pode utilizar um APPLET para ajudar a encontrar uma solução do problema. É só clicar no botão abaixo!

Solução

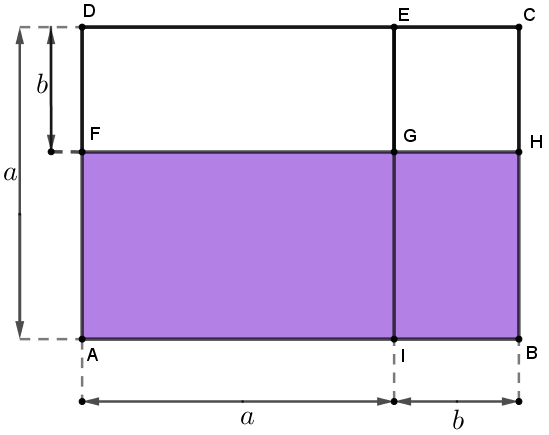
Observando a figura abaixo, vemos que, geometricamente a área

$S_{ABHF}$ do retângulo roxo pode ser calculada como a diferença entre as áreas

$S_{ABCD}$ e

$S_{FHCD}$ respectivas dos também retângulos

$ABCD$ e

$FHCD$ , o que nos fornece a igualdade:

$\qquad S_{ABHF}=S_{ABCD}-S_{FHCD}.\qquad \textcolor{#9966FF}{(i)}$
Particularmente, a área do retângulo

$FHCD$ é a soma das áreas do retângulo

$FGED$ e do quadrado

$GHCE$ , ou seja:

$\qquad S_{FHCD}=S_{FGED}+S_{GHCE}.\qquad \textcolor{#9966FF}{(ii)}$
Portanto, das igualdades

$\textcolor{#9966FF}{(i)}$ e

$\textcolor{#9966FF}{(ii)}$ , segue que:

$\qquad S_{ABHF}=S_{ABCD}-\left(S_{FGED}+S_{GHCE}\right)\\ \qquad S_{ABHF}=S_{ABCD}-S_{FGED}-S_{GHCE} .\qquad \textcolor{#9966FF}{(iii)}$
Mas, a partir das medidas

$a$ e

$b$ definidas na mesma figura, podemos reescrever algebricamente a igualdade

$\textcolor{#9966FF}{(iii)}.$ Observe

$\qquad S_{ABHF}=S_{ABCD}-S_{FGED}-S_{GHCE} \\ \qquad (a+b) \cdot (a-b)= a \cdot (a+b) -a \cdot b- b^2\\ \qquad (a+b) \cdot (a-b)= a^2 +a \cdot b -a \cdot b- b^2\\ \qquad (a+b) \cdot (a-b)= a^2 – b^2.$
A igualdade

$\boxed{ (a+b) \cdot (a-b)= a^2 – b^2}$ obtida nada mais é do que o produto notável denominado produto da soma pela diferença de dois termos.