(A) Problema para ajudar na escola: Uma área alaranjada

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)

---

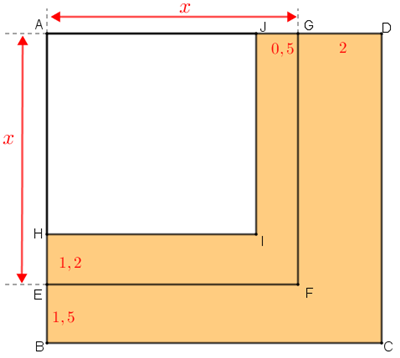
Na figura, podemos ver três retângulos (particularmente, [tex]AEFG[/tex] é um quadrado).
Se os comprimentos dos lados desses retângulos estão expressos em metros, determinar o valor de [tex]x[/tex], para que a área da região colorida seja [tex]2.072 \, m^2[/tex].

Solução

---

Para facilitar a interpretação geométrica do problema, vamos denotar por [tex]A_1 \, [/tex] e [tex] \, A_2 \, [/tex] as áreas dos retângulos [tex]AHIJ \, [/tex] e [tex]ABCD \, [/tex], respectivamente, conforme ilustra a figura abaixo.
Observe que se [tex]A[/tex] é a área da região colorida, então [tex]\boxed{A=A_2-A_1} \, .[/tex]

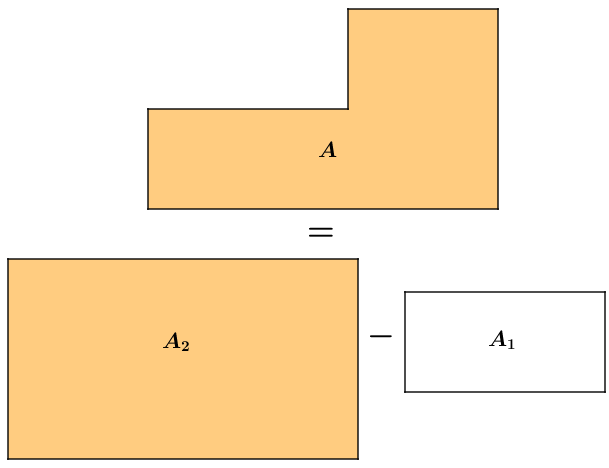
Assim, como já temos a área [tex]A[/tex], devemos obter as áreas [tex]A_1 \, [/tex] e [tex] \, A_2 \, .[/tex] Vamos lá!

• Área [tex]A_1 \, [/tex]
  Veja que os comprimentos em metros dos lados do retângulo [tex]AHIJ \, [/tex] são [tex]x-1,2[/tex] e [tex]x-0,5[/tex]. Assim:
  [tex]\qquad A_1=\left(x-1,2\right) \cdot \left(x-0,5\right)[/tex]
  [tex]\qquad \boxed{A_1=x^2-1,7x+0,6} \, .[/tex]
• Área [tex]A_2 \, [/tex]
  Note que os comprimentos em metros dos lados do retângulo [tex]ABCD \, [/tex] são [tex]x+2[/tex] e [tex]x+1,5[/tex]. Logo:
  [tex]\qquad A_2=\left(x+1,5\right) \cdot \left(x+2\right)[/tex]

[tex]\qquad \boxed{A_2=x^2+3,5x+3} \, .[/tex]

Com isso,
[tex]\qquad A=A_2-A_1[/tex]
[tex]\qquad 2072=\left(x^2+3,5x+3 \right) – \left(x^2-1,7x+0,6 \right)[/tex]
[tex]\qquad 2072=\cancel{x^2}+3,5x+3-\cancel{x^2}+1,7x-0,6[/tex]
[tex]\qquad 2072=5,2x+2,4[/tex]
[tex]\qquad 2072-2,4=5,2x[/tex]
[tex]\qquad 2069,6=5,2x[/tex]
[tex]\qquad x=\dfrac{2069,6}{5,2}=398 \, .[/tex]
Portanto o valor de [tex]x[/tex] para que a área da região colorida seja [tex]2.072 \, m^2[/tex] é [tex] \, \fcolorbox{black}{#fda}{$x=398 \, m$} \, .[/tex]

---

Solução elaborada pelos Moderadores do Blog.