✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 2º ano do E. M.)
Vamos considerar uma forma especial de cobrir ou pavimentar o plano usando polígonos regulares. Uma pavimentação será válida se satisfizer as seguintes condições:
(i) Estar formada por exatamente dois tipos de polígonos regulares diferentes com lados medindo uma unidade de medida;
(ii) A interseção de dois polígonos é sempre um lado ou um vértice ou vazia;
(iii) Cada um dos vértices deve ser vértice comum do mesmo número de polígonos de cada tipo, ou seja, a distribuição ao redor de cada vértice é sempre a mesma.
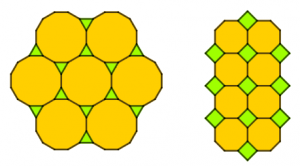
Na figura a seguir vemos três formas diferentes de pavimentar o plano, usando polígonos regulares, que satisfazem a estas condições.

Encontre mais duas pavimentações do plano que satisfazem às condições (i), (ii) e (iii).
Solução
Vamos usar o fato de que o ângulo interno de um polígono regular de [tex]n[/tex] lados mede [tex]\dfrac{(n-2)180^\circ}{n}[/tex].
Consideremos uma pavimentação geral em que cada vértice seja vértice comum de [tex]m[/tex] polígonos regulares de [tex]n[/tex] lados e de [tex]k[/tex] polígonos regulares de [tex]h[/tex] lados. Por exemplo, na primeira pavimentação da figura do enunciado cada vértice é vértice comum de [tex]1[/tex] hexágono regular ([tex]6[/tex] lados) e de [tex]4[/tex] triângulos equiláteros ([tex]3[/tex] lados); na segunda pavimentação, cada vértice é vértice comum de [tex]2[/tex] quadrados ([tex]4[/tex] lados) e de [tex]3[/tex] triângulos equiláteros ([tex]3[/tex] lados), etc. Observe que a soma de todos os ângulos internos com vértice em comum somam [tex]360^\circ[/tex].
Nossa pavimentação geral deve satisfazer a seguinte equação:
[tex]\qquad \dfrac{m(n-2)180^\circ}{n}+\dfrac{k(h-2)180^\circ}{h}=360^\circ[/tex]
[tex]\qquad \dfrac{m(n-2)}{n}+\dfrac{k(h-2)}{h}=2[/tex]
[tex]\qquad \boxed{mh(n-2)+kn(h-2)=2nh}.[/tex]
É importante ressaltar que toda pavimentação satisfazendo às condições (i), (ii) e (iii) fornece uma solução nos inteiros positivos para esta equação, entretanto essa equação possui soluções inteiras positivas que não originam pavimentações válidas. Por exemplo, [tex]m=2[/tex], [tex]n=4[/tex], [tex]k=2[/tex] e [tex]h=4[/tex] é uma solução para a equação acima, mas a pavimentação gerada usa apenas quadrados, não sendo válida por não verificar a condição (i). Mas pelo menos sabemos que as pavimentações que buscamos estão entre as soluções da equação acima.
De uma forma geral, essa é uma equação difícil de se resolver. Porém, estamos procurando por soluções inteiras positivas dessa equação. Vamos supor, sem perda de generalidade, que [tex]m\geq k[/tex].
- Pela condição (i) teremos pelo menos um polígono de cada tipo; assim sendo, vamos começar analisando a possibilidade [tex]m=k=1[/tex]. Neste caso,
[tex]\qquad h(n-2)+n(h-2)=2nh[/tex]
[tex]\qquad nh-2h+nh-2n=2nh[/tex]
[tex]\qquad h+n=0.[/tex]
Como o número de lados deve ser inteiro positivo, vemos que não temos uma pavimentação no caso [tex]m=k=1[/tex]. - Vamos agora ao caso [tex]m=2[/tex] e [tex]k=1[/tex]. Neste cenário
[tex]\qquad 2h(n-2)+n(h-2)=2nh[/tex]
[tex]\qquad 2nh-4h+nh-2n=2nh[/tex]
[tex]\qquad -4h+nh-2n=0.[/tex]
Vale lembrar que [tex]h[/tex] representa o número de lados de um polígono regular, ou seja, é um número inteiro maior do que [tex]2[/tex]. Portanto, devemos substituir os valores [tex]h=3, 4, 5, \dots[/tex]
[tex]\qquad \rhd[/tex] [tex]h=3[/tex]
[tex]\qquad -12+3n-2n=0[/tex]
[tex]\qquad n=12.[/tex]
Encontramos uma solução nos inteiros positivos para nossa equação. Como a figura abaixo mostra, essa solução gera uma pavimentação que satisfaz as condições (i), (ii) e (iii) em que cada vértice é vértice comum de [tex]2[/tex] polígonos regulares de [tex]12[/tex] lados e [tex]1[/tex] triângulo equilátero.
[tex]\qquad \rhd[/tex] [tex]h=4[/tex]
[tex]\qquad -16+4n-2n=0[/tex]
[tex]\qquad n=8.[/tex]
Encontramos outra solução nos inteiros positivos que gera uma pavimentação que satisfaz as condições (i), (ii) e (iii) em que cada vértice é vértice comum de [tex]2[/tex] octógonos regulares e [tex]1[/tex] quadrado.
[tex]\qquad \rhd[/tex] [tex]h=5[/tex]
[tex]\qquad -20+5n-2n=0[/tex]
[tex]\qquad n=20/3.[/tex]
Não é uma solução inteira.
[tex]\qquad \rhd[/tex] [tex]h=6[/tex]
[tex]\qquad -24+6n-2n=0[/tex]
[tex]\qquad n=6.[/tex]
Essa solução não gera uma pavimentação válida, pois cada vértice é vértice comum de [tex]2[/tex] hexágonos regulares e [tex]1[/tex] hexágono regular, ou seja, só estamos usando hexágonos e, desta maneira, violando à condição (i).
As soluções [tex]m=2[/tex], [tex]n=12[/tex], [tex]k=1[/tex], [tex]h=3[/tex] e [tex]m=2[/tex], [tex]n=8[/tex], [tex]k=1[/tex], [tex]h=4[/tex] dão origem às pavimentações mostradas na próxima figura.
Solução elaborada pelos Moderadores do Blog.
