✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir da 1ª série do E.M.)
Johannes Kepler ([tex]1571 – 1630[/tex]), um matemático e astrônomo alemão, por meio de estudos, conseguiu estabelecer três Leis sobre o movimento dos planetas do nosso sistema solar. Essas Leis foram a principal contribuição de Kepler à mecânica celeste.
A primeira Lei, mais conhecida como Lei das Órbitas, diz que:
- Os planetas descrevem ao redor do Sol trajetórias elípticas, e o Sol ocupa um dos focos dessa elipse.
Considere a representação abaixo, de metade da órbita do planeta Mercúrio em torno do Sol. A distância [tex]r_{M}[/tex] entre o Sol e Mercúrio varia em função do ângulo [tex]\theta[/tex], sendo [tex]0 ^\circ \leq \theta \leq 180 ^\circ [/tex].
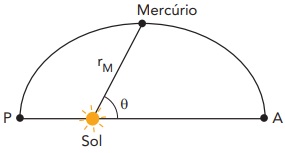
Para o cálculo aproximado de [tex]r_{M}[/tex], em milhões de quilômetros, emprega-se a seguinte fórmula:
[tex]\qquad r_{M}=\dfrac {555}{10-2 \cdot cos \theta}.[/tex]
Os pontos [tex]P[/tex] (periélio) e [tex]A[/tex] (afélio) são os pontos onde Mercúrio encontra-se mais próximo do Sol e mais afastado, respectivamente. Encontre a distância aproximada entre esses pontos.
(Adaptado de UERJ).
Solução
Para encontrarmos a que distância do Sol está Mercúrio no ponto [tex]A[/tex], basta fazer [tex]\theta=0^\circ[/tex].
Assim:
[tex]\qquad r_{A}=\dfrac {555}{10-2 \cdot cos 0^\circ}\\
\qquad r_{A}=\dfrac {555}{10-2 \cdot 1}=\dfrac {555}{8}\\
\qquad \boxed{r_{A}=69,375}.[/tex]
Para encontrarmos a que distância do Sol está Mercúrio no ponto [tex]P[/tex], basta fazer [tex]\theta=180^\circ[/tex].
Assim:
[tex]\qquad r_{P}=\dfrac {555}{10-2 \cdot cos 180^\circ}\\
\qquad r_{P}=\dfrac {555}{10-2 \cdot (-1)} =\dfrac {555}{12}\\
\qquad \boxed{r_{P}=46,25}.[/tex]
Logo, a distância aproximada entre os pontos [tex]P[/tex] e [tex]A[/tex] é de
[tex]\qquad 69,375 + 46,25 = 115,625[/tex] milhões de quilômetros.
Solução elaborada pelos Moderadores do Blog.
