Clique no botão abaixo para visualizar o problema.
Problema
Na figura abaixo, G, H, I, J, K e L são os pontos médios dos lados do hexágono ABCDEF.
O hexágono foi dividido em seis quadriláteros, dos quais cinco deles já estão com suas respectivas áreas apresentadas em seus interiores.
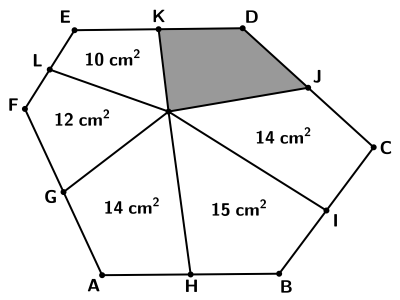
Determine a área da região sombreada, em cm².
Solução 1
Vamos traçar segmentos de reta com extremidades nos vértices do hexágono e no ponto no interior do hexágono. Assim, cada quadrilátero ficará dividido em dois triângulos.
Observe que:
- os triângulos que têm um dos lados sobre um mesmo lado do hexágono devem ter mesma área, pois eles possuem a base e a altura de mesma medida;
- os triângulos que possuem um lado em comum e formam um quadrilátero na figura inicial, devem ter juntos a mesma área do quadrilátero.
Assim, se os dois triângulos congruentes definidos a partir dos pontos E, K e D têm área x, podemos representar as áreas de cada triângulo conforme mostra a figura abaixo.
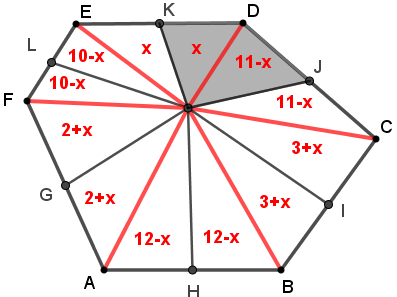
Logo, a área da região sombreada é [tex]\boxed{x+(11-x)}[/tex], ou seja, [tex]~\fcolorbox{black}{#DAE2E7}{$11\text{ cm}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Chamaremos de [tex]O[/tex] o ponto interno ao hexágono no qual os segmentos que partem dos pontos médios dos lados se tocam. Em seguida, ligaremos os vértices [tex]A, B, C, D, E[/tex] e [tex]F[/tex] ao ponto [tex]O[/tex]. Daí, teremos vários triângulos, dos quais analisaremos as suas áreas.
Como é sabido, a mediana de um triângulo o divide em dois triângulos menores de áreas equivalentes; logo, utilizando esse raciocínio, analisaremos o triângulo [tex]AOB[/tex].
- Como [tex]OH[/tex] é mediana (pois [tex]H[/tex] é ponto médio do segmento [tex]AB[/tex]), os triângulos [tex]AOH[/tex] e [tex]BOH[/tex] terão áreas iguais.
Utilizando esse raciocínio, fizemos o mesmo com os demais triângulos, como mostra a figura a seguir.
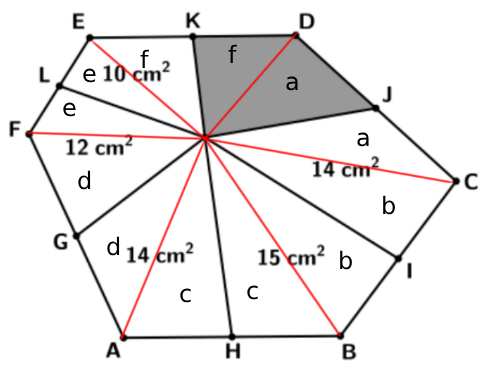
Denotamos as áreas por letras minúsculas para não confundirmos com os vértices.
Observando a imagem, é fácil perceber que:
- [tex]a+b=14[/tex]
- [tex]b+c=15[/tex]
- [tex]c+d=14[/tex]
- [tex]d+e =12[/tex]
- [tex]e+f =10.[/tex]
Daí, percebe-se também que é possível calcular a área desse hexágono somando os valores das áreas de [tex]a[/tex] a [tex]f[/tex] e multiplicando esse valor por dois, pois cada área dessa é duplicada. Assim, temos:
[tex]\qquad Total = 2\cdot (a+b+c+d+e+f) = 2\cdot (14+14+10)\\
\qquad Total = 76\text{ cm}^2.[/tex]
Como a área que queremos é a sombreada, basta calcular a diferença entre a área total e a área não sombreada. Sem dificuldades, percebemos que a área clara é [tex]65\text{ cm}^2[/tex], portanto, a área sombreada ([tex]S[/tex]), é
[tex]\qquad S = 76-65\\
\qquad \fcolorbox{black}{#DAE2E7}{$S=11\text{ cm}^2$}\,.[/tex]
Solução elaborada pelo COM Phidias.
Nível B – Questão Difícil
