Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 2º ano do E. M.)
(Unicamp, 2020 – Adaptado) A figura a seguir representa um triângulo isósceles com dois lados medindo [tex]5 \;cm[/tex] e o ângulo formado por estes lados medindo [tex]\theta[/tex].
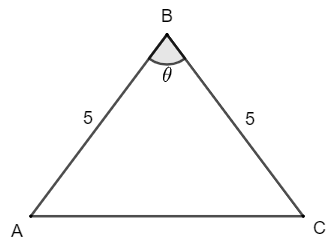
Sabendo que [tex]\cos \theta = \dfrac{3}{5}[/tex], determine:
a) A área desse triângulo.
b) O comprimento do raio da circunferência circunscrita a esse triângulo.

Lembretes
(I) Relação Fundamental da Trigonometria:
[tex]\qquad \text{sen}^2\, \alpha+\cos^2\,\alpha=1[/tex], para qualquer medida angular [tex]\alpha[/tex].
(II) Conhecidas as medidas [tex]a[/tex] e [tex]b[/tex] de dois lados de um triângulo [tex]ABC[/tex] qualquer e a medida [tex]\alpha[/tex] do ângulo compreendido entre estes lados, a área de [tex]ABC[/tex] é dada por
[tex]\qquad A_r(ABC) = \dfrac{1}{2}\cdot a\cdot b\cdot sen \; \alpha[/tex].
(III) (Lei dos Cossenos) Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] valem as relações:
[tex]\qquad {\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos{\widehat {A}}\,\!}[/tex];
[tex]\qquad {\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot cos{\widehat {B}}\,\!}[/tex];
[tex]\qquad {\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot cos{\widehat {C}}\,\!}[/tex].
(IV) (Lei dos Senos) Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] vale a relação:
[tex]\qquad \dfrac{a}{sen \;\hat{A}} = \dfrac{b}{sen \;\hat{B}} = \dfrac{c}{sen \;\hat{C}} = 2R[/tex],
sendo [tex]R[/tex] o raio da circunferência circunscrita ao triângulo [tex]ABC[/tex].
Solução 1
a) Como [tex]\cos \theta = \dfrac{3}{5}[/tex], pela Relação Fundamental da Trigonometria segue que:
[tex]\qquad sen^2 \;\theta +\cos^2 \theta = 1[/tex]
[tex]\qquad sen^2 \;\theta+\left(\dfrac{3}{5}\right)^2=1[/tex]
[tex]\qquad sen^2 \;\theta=1-\left(\dfrac{3}{5}\right)^2 = \dfrac{16}{25}[/tex]
[tex]\qquad sen \;\theta = \pm\dfrac{4}{5}.[/tex]
Como [tex]\theta\lt 180^{\circ}[/tex], devemos ter [tex]sen \;\theta = \dfrac{4}{5}.[/tex]
Pelo Lembrete (II), a área do triângulo [tex]ABC[/tex] é dada por
[tex]\qquad A_r(ABC) = \dfrac{1}{2}\cdot 5\cdot 5\cdot sen \;\theta[/tex]
[tex]\qquad A_r(ABC) = \dfrac{1}{2}\cdot 5\cdot 5\cdot \dfrac{4}{5}[/tex]
[tex]\qquad \boxed{A_r(ABC) = 10 \text{ cm}^2}.[/tex]
b) Seja [tex]l[/tex] a medida do lado [tex]AC[/tex]; então, pela Lei dos Cossenos, temos:
[tex]\qquad\begin{align}l^2 &= 5^2+5^2-2\cdot 5\cdot 5\cdot \cos \theta \\
&= 5^2+5^2-2\cdot 5\cdot 5\cdot \dfrac{3}{5}\\
&= 25+25-50\cdot \dfrac{3}{5}\\
&= 20.
\end{align}[/tex]
Assim, [tex]l = 2\sqrt{5} \text{ cm}.[/tex]
Finalmente, sendo [tex]R[/tex] o raio da circunferência circunscrita ao triângulo, temos, pela Lei dos Senos, que:
[tex]\qquad \dfrac{l}{sen\;\theta} = 2R\\
\qquad 2R = \dfrac{2\sqrt{5}}{\frac{4}{5}}\\
\qquad \boxed{R = \dfrac{5\sqrt{5}}{4} \text{ cm}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
A princípio, chamaremos os dois lados iguais de [tex]a[/tex] e [tex]b[/tex] e a base do triângulo de [tex]c[/tex].
a) Podemos utilizar a fórmula para se obter a área de um triângulo usando seno: [tex]A = \dfrac{a \cdot b \cdot sen\theta}{2}~~[/tex] (i).
Como temos apenas o valor de [tex]cos \theta[/tex], podemos encontrar [tex]sen \theta[/tex] utilizando a lei fundamental da trigonometria:
[tex]\qquad sen^2\theta + cos^2\theta = 1[/tex]
[tex]\qquad sen^2\theta = 1-cos^2\theta.[/tex]
Desenvolvendo e observando que [tex] sen\theta \gt 0[/tex] temos:
[tex]\qquad sen^2\theta = 1-\left(\dfrac{3}{5}\right)^2\\
\qquad sen^2\theta = 1-\dfrac{9}{25}\\
\qquad sen^2\theta = \dfrac{25}{25}-\dfrac{9}{25}\\
\qquad sen^2\theta = \dfrac{16}{25}\\
\qquad sen\theta = \sqrt{\dfrac{16}{25}}[/tex]
[tex]\qquad sen \theta = \dfrac{4}{5}.~~~~~[/tex] (ii)
Substituindo (ii) em (i), ficamos com:
[tex]\qquad A =\dfrac{a \cdot b \cdot sen\theta}{2}\\
\qquad A=\dfrac{5 \cdot 5}{2}\cdot \dfrac{4}{5}\\
\qquad A=5 \cdot 2\\
\qquad A=10\text{ cm}^2.[/tex]
b) Podemos descobrir o raio da circunferência circunscrita utilizando a lei dos senos; porém, para isso, precisamos do valor da base [tex]c[/tex]. Iremos descobrir aplicando a lei dos cossenos em [tex]c[/tex]:
[tex]\qquad c^2 = a^2 + b^2 – 2ab \cdot cos\theta\\
\qquad c^2 = 5^2 + 5^2 – 2 \cdot 5 \cdot 5 \cdot \dfrac{3}{5}\\
\qquad c^2 = 25 + 25 – 2 \cdot 5 \cdot \cancel{5} \cdot \dfrac{3}{\cancel{5}}\\
\qquad c^2 = 50 – 2 \cdot 5 \cdot 3\\
\qquad c^2 = 50 – 30\\
\qquad c^2 = 20\\
\qquad c = \sqrt{20}\\
\qquad c = \sqrt{2 \cdot 2 \cdot 5}[/tex]
[tex]\qquad c = 2\sqrt{5}.~~~~~~~~ [/tex](iii)
Agora, podemos aplicar a lei dos senos, utilizando (ii) e (iii), sendo [tex]r[/tex] o raio da circunferência circunscrita:
[tex]\qquad \dfrac{c}{sen\theta} = 2r\\
\qquad \dfrac{2\sqrt{5}}{\frac{4}{5}} = 2r\\
\qquad 2\sqrt{5} \cdot \dfrac{5}{4} = 2r\\
\qquad \dfrac{10\sqrt{5}}{4} = 2r\\
\qquad \dfrac{5\sqrt{5}}{2} = 2r\\
\qquad r = \dfrac{5\sqrt{5}}{2 \cdot 2}\\
\qquad r = \dfrac{5\sqrt{5}}{4} \text{ cm}.[/tex]
Assim, concluímos que o triângulo da figura possui uma área de [tex]10\text{ cm}^2[/tex] e sua circunferência circunscrita tem um raio de [tex]\dfrac{5\sqrt{5}}{4}\text{ cm}.[/tex]
Solução elaborada pelo COM Potências de Euler.
Solução 3
a) Utilizando a lei dos cossenos para determinar o lado AC, temos:
[tex]\qquad AC^2 = 5^2 + 5^2 -2\cdot 5\cdot 5\cdot \dfrac{3}{5} = 50 – 30 = 20 \\
\qquad AC = 2\sqrt{5}.[/tex]
Daí, para determinarmos a área do triângulo, traçamos a altura relativa à base AC. Chamaremos o ponto médio de AC de M. O segmento BM é altura e também mediana; logo, podemos aplicar o teorema de Pitágoras no triângulo BMC, de hipotenusa medindo [tex]5 cm[/tex], cateto [tex]\sqrt{5}[/tex] e altura BM. Segue:
[tex]\qquad BM^2 = 5^2 – (\sqrt{5})^2 = 25 – 5 = 20 \\
\qquad BM = 2\sqrt{5}.[/tex]
Portanto, temos que a área do triângulo será:
[tex]\qquad A = \dfrac{2\sqrt{5}\cdot 2 \sqrt{5}}{2}= \dfrac{4\cdot 5}{2} = 10\text{cm}^2.[/tex]
b) Observando o triângulo BMC criado, como ele é retângulo, temos, por definição da razão trigonométrica seno, que:
[tex]\qquad sen C = \dfrac{BM}{BC} = \dfrac{2\sqrt{5}}{5}.[/tex]
Portanto, para encontrar o raio da circunferência circunscrita, usamos a lei dos senos:
[tex]\qquad 2R=\dfrac{AB}{sen C} = \dfrac{5}{\frac{2\sqrt{5}}{5}} = \dfrac{25}{2\sqrt{5}} =\dfrac{25\sqrt{5}}{2\cdot 5} = \dfrac{5\sqrt{5}}{2}. [/tex]
Portanto, [tex] \boxed{R = \dfrac{5\sqrt{5}}{4}\text{cm}}.[/tex]
Solução elaborada pelo COM Phidias, com contribuições dos Moderadores do Blog.
