Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
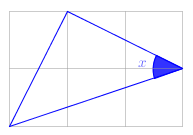
(OPM 2015 – adaptado) Em uma folha de papel quadriculado, Julinho desenhou um triângulo, tal como o mostrado na figura.
Determine a amplitude [tex]x[/tex] do ângulo assinalado.
Solução
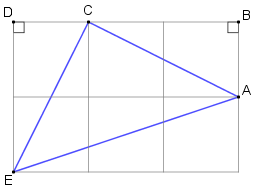
Como o desenho foi feito em uma folha de papel quadriculado, podemos observar vários triângulos retângulos, entre eles os triângulos [tex]ABC[/tex] e [tex]CDE[/tex]. Perceba que esses dois triângulos têm catetos com mesma medida; assim, pelo caso de congruência L.A.L, eles são congruentes.
Com isso podemos concluir que:
- os ângulos [tex]C\hat{E}D[/tex] e [tex]A\hat{C}B[/tex] têm a mesma medida;
- os ângulos [tex]D\hat{C}E[/tex] e [tex]B\hat{A}C[/tex] têm a mesma medida;
- os segmentos [tex]\overline{CE}[/tex] e [tex]\overline{CA}[/tex] têm o mesmo comprimento.
Assim, o triângulo [tex]CAE[/tex] é isósceles e, portanto, os ângulos da base são congruentes.
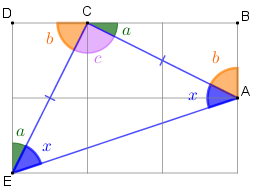
Por outro lado, sabemos que a soma dos ângulos internos de um triângulo é igual a [tex]180^{\circ}[/tex], portanto, considerando as medidas, em graus, registradas na figura acima, segue que
[tex]\qquad 180^{\circ}= x+c+x[/tex]
[tex]\qquad 180^{\circ}= 2x+c[/tex]
Observe também na figura que [tex]b+c+a=180^{\circ}[/tex]; logo, [tex]c=180^{\circ}-b-a[/tex] e com isso:
[tex]\qquad 180^{\circ}= 2x+\left(180^{\circ}-b-a\right)[/tex]
[tex]\qquad 2x=b+a. \quad \textcolor{#800000}{(i)}[/tex]
Perceba, agora, que [tex]a[/tex] e [tex]b[/tex] são medidas de ângulos agudos internos de triângulos retângulos, logo [tex]a+b+90^{\circ}=180^{\circ}[/tex] e [tex]a+b=90^{\circ}.[/tex] Assim, segue de [tex]\textcolor{#800000}{(i)}[/tex] que [tex]2x=90^{\circ}[/tex], e, finalmente, temos que [tex]\fcolorbox{black}{#eee0e5}{$x=45^{\circ}$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
