Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
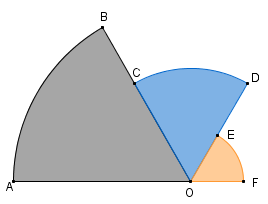
Qual é a área da região colorida mostrada na figura, sabendo-se que [tex]\stackrel{\frown}{AB}[/tex], [tex]\stackrel{\frown}{CD}[/tex] e [tex]\stackrel{\frown}{EF}[/tex] são arcos de [tex]60^{\circ}[/tex] definidos por circunferências de centros em [tex]O[/tex] e cujos raios medem [tex]3[/tex], [tex]2[/tex] e [tex]1[/tex] centímetros, respectivamente?

Lembretes
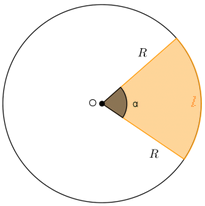
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] graus:
[tex]\qquad \qquad \boxed{A_{setor}=\dfrac{\pi\cdot R^{\,2} \cdot \alpha}{360}}[/tex]
(Para aprender um pouco mais sobre setor circular, clique AQUI.)
Solução
Perceba que a figura é composta por três setores circulares com ângulos centrais de [tex]60^{\circ}.[/tex] (Lembre-se de que a medida em graus de um ângulo central é a medida do arco correspondente.) Assim, a área [tex]S[/tex] da região colorida mostrada na figura é a soma das áreas dos setores circulares [tex]OAB[/tex], [tex]OCD[/tex], [tex]OEF[/tex], que é igual a:
[tex]\qquad \begin{align*} S&=\dfrac{\pi\cdot 3^{2}\cdot 60}{360}+\dfrac{\pi\cdot 2^{2}\cdot 60}{360}+\dfrac{\pi\cdot 1^{2}\cdot 60}{360}\\
&=\dfrac{\pi\cdot 3^{2}}{6}+\dfrac{\pi\cdot 2^{2}}{6}+\dfrac{\pi\cdot 1^{2}}{6}\\
&=\dfrac{\pi}{6}\left(3^2+2^2+1^2\right)\\
&=\dfrac{14\pi}{6}\\
&=\dfrac{7\pi}{3}.
\end{align*}[/tex]
Portanto, a área da região em questão é [tex]\fcolorbox{black}{#eee0e5}{$\dfrac{7\pi}{3}\,cm^2$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
