✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
Um agricultor tem um grande terreno e gostaria de delimitar nele uma área retangular para formar um pomar.
Nos fundos do terreno há um muro, a partir do qual ele delimitará a área desejada, e, para cercar os outros três lados, o agricultor tem disponível [tex]100\;m[/tex] de tela metálica.
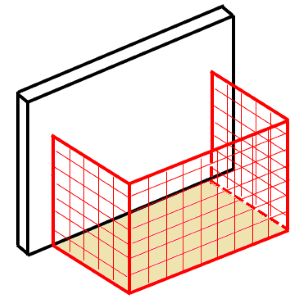
Quais devem ser as dimensões do terreno a ser cercado, para que o futuro pomar tenha área máxima?

Lembrete
Uma função polinomial do segundo grau definida [tex]f[/tex] por [tex]f(x) = ax^2+bx+c[/tex], com [tex]a<0[/tex], admite valor máximo em [tex]x = \dfrac{-b}{2a}[/tex].
Solução
Seja [tex]x[/tex] a medida em metros dos lados opostos que serão cercados. Então, o terceiro lado deve medir [tex]100-2x[/tex] metros.
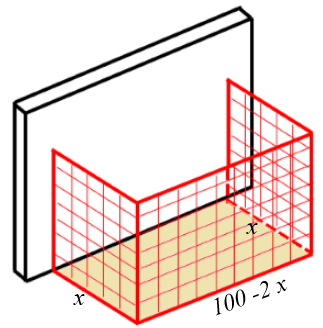
Assim, a área da região que será cercada é dada em função de [tex]x[/tex] na forma [tex]A(x) = x(100-2x) = -2x^2+100x[/tex].
Pelo Lembrete, esta função área [tex]A[/tex] terá valor máximo em [tex]x = \dfrac{-100}{2(-2)} = 25[/tex].
Logo, para que o pomar tenha área máxima, o terreno retangular a ser cercado é um terreno [tex]25\;m \times 50\,m[/tex]; mas lembrem-se de que apenas três lados desse terreno serão cercados.
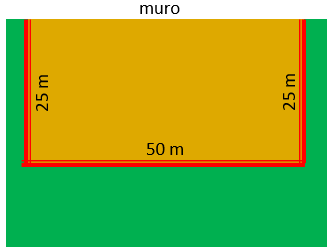
Solução elaborada pelos Moderadores do Blog.
