O problema de Monty Hall
Este é um problema matemático inspirado no jogo "Let’s Make a Deal" de um programa de televisão dos Estados Unidos exibido na década de 1970 e apresentado por Monty Hall.
 Imagem extraída de https://cityobservatory.org/such-a-deal/
Imagem extraída de https://cityobservatory.org/such-a-deal/
Eis o problema:
– Atrás de uma dessas portas tem um carro; mas atrás de cada uma das outras duas tem um bode. Escolha uma porta e leve para casa o que estiver atrás dela.

Você vai lá e escolhe uma das três portas; mas antes que você possa abri-la, o apresentador (que sabe exatamente onde está o carro) pede para você esperar e ele abre uma das portas não escolhidas, mostrando um dos bodes. Nesse momento ele faz a seguinte pergunta a você:
– Você quer ficar com a porta que você escolheu ou quer trocá-la pela outra porta fechada?
Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente ou mudar de porta?
Solução
Em um primeiro momento você pode pensar:
– "Ah! Agora eu tenho duas portas para escolher:
• se eu ficar com a porta que eu escolhi, eu tenho [tex]50\%[/tex] de chance de pegar o carro;
• se eu trocar de porta, eu continuo com [tex]50\%[/tex] de chance pegar o carro.
Então tanto faz trocar ou não trocar: é só uma questão de sorte…"
Mas essa análise está errada!
Na situação proposta no problema, a melhor coisa a fazer é trocar de porta; pois, com a troca, a chance de ganhar passa de [tex]\mathbf{\dfrac{1}{3}}[/tex] para [tex]\mathbf{\dfrac{2}{3}}.[/tex]
Não se sinta diminuído(a) se você continuar pensando que tanto faz, mesmo vendo a resposta "seca" de que a troca é mais vantajosa…
Em 1990, em resposta a um leitor, a escritora norte-americana Marilyn vos Savant, a pessoa de QI mais elevado do mundo à época, publicou a solução do problema de Monty Hall em sua coluna "Ask Marilyn", na revista Parade. Em sua resposta, Marilyn apontou que o certo era fazer a troca, e recebeu mais de 10 mil cartas de protesto. Muitas foram escritas até por matemáticos e físicos, alguns com Doutorado, garantindo que o correto era não trocar a porta inicialmente escolhida. As coisas só se acalmaram por lá após Marilyn recomendar que as pessoas simulassem o jogo, repetindo várias vezes cada uma das estratégias e verificando a taxa de sucesso de cada uma!
A resposta do problema é, de fato, bem contra intuitiva; mas vejamos algumas justificativas para ela.
Não existe razão para que essa probabilidade mude após o apresentador ter aberto uma das portas não premiadas e, quando uma dessas portas é aberta (por esconder um bode), a porta não escolhida que continua fechada passa a acumular [tex]\dfrac{2}{3}[/tex] da probabilidade de ser a porta que esconde o carro.
Suponhamos [tex]1\,000[/tex] portas: em uma porta tem um carro e nas outras [tex]999[/tex] têm bodes.
Escolhemos uma dessas [tex]1\,000[/tex] portas e o apresentador abre [tex]998[/tex] portas com bodes; ficam fechadas só a porta escolhida e mais uma, sendo que uma tem um bode e uma tem um carro.
Inicialmente, a probabilidade de termos escolhido o carro em [tex]1\,000[/tex] portas era uma em mil, isto é, [tex]\frac{1}{1000}= 0,1\%.[/tex] Então, a chance de ter um carro em outra porta era [tex]99,9\%.[/tex] Dessa forma, depois de abertas as [tex]998[/tex] portas com bodes, a sua escolha é: [tex]0,1\%[/tex] ou [tex]99,9\%[/tex] de probabilidade de ganhar o carro!
Sim, trocar é a melhor opção!
Observe que existem duas escolhas a serem feitas: uma escolha inicial, aleatória, e uma segunda, após o apresentador abrir uma das portas e perguntar se gostaríamos de mudar a porta inicialmente escolhida.
Então a nossa árvore terá duas etapas de construção e com ela calcularemos a probabilidade de ganharmos o carro.
As primeiras probabilidades são relativas à escolha da porta:
• a probabilidade de escolhermos inicialmente o carro é de [tex]\frac{1}{3}[/tex],
• a probabilidade de escolhermos um bode é de [tex]\frac{2}{3}[/tex], consequentemente.
Para a segunda fase do desafio, temos que analisar os casos em que mudamos ou não de opinião.
• Para o caso de termos escolhido inicialmente a porta do carro, se mantivermos a escolha, é certo que ganharemos o carro; assim, a probabilidade condicional [tex]P(\text{Manter}|{Carro})[/tex] será [tex]1=100\%[/tex]. Por outro lado, se mudarmos de porta, acabamos por invariavelmente perder o carro, ou seja, a probabilidade condicional [tex]P(\text{Trocar}|{Carro})[/tex] é nula.
• Ao escolhermos inicialmente um bode, se mantivermos a escolha, não ganharemos o carro; assim, a probabilidade condicional [tex]P(\text{Manter}|{Bode})[/tex] será zero. Por outro lado, se mudarmos de porta, vamos ganhar o carro; assim, a probabilidade condicional [tex]P(\text{Trocar}|{Bode})[/tex] será [tex]1=100\%[/tex].
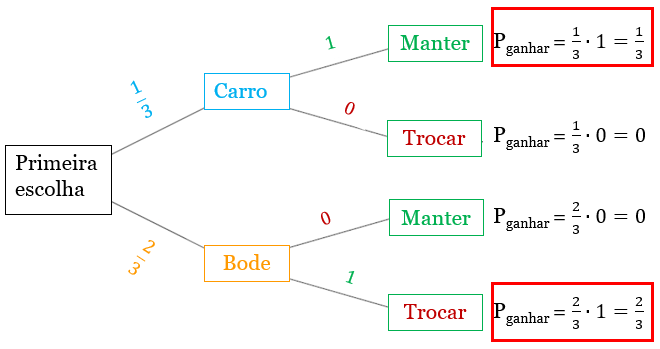
Concluímos, então, que a probabilidade de ganharmos o carro mantendo a porta inicialmente escolhida é [tex]\dfrac{1}{3}[/tex], enquanto que a probabilidade de ganharmos trocando a porta inicialmente escolhida é [tex]\dfrac{2}{3}.[/tex]
Vamos supor, sem perda de generalidade, que escolhemos a porta [tex]1[/tex]. (O "sem perda de generalidade" significa que o raciocínio que desenvolveremos seria o mesmo se a porta escolhida fosse a [tex]2[/tex] ou a [tex]3[/tex].)
Nesse caso, consideremos os seguintes eventos, dois a dois disjuntos:
[tex]\qquad C1[/tex]: o carro está atrás da porta [tex]1[/tex];
[tex]\qquad C2[/tex]: o carro está atrás da porta [tex]2[/tex];
[tex]\qquad C3[/tex]: o carro está atrás da porta [tex]3[/tex].
Escolhida a porta, o apresentador abre uma das outras portas que não tenha o carro, Suponhamos, sem perda de generalidade, que o apresentador tenha aberto a porta [tex]3[/tex]. (O "sem perda de generalidade" significa aqui que o raciocínio que desenvolveremos seria o mesmo se a porta aberta pelo apresentador fosse a [tex]2[/tex].)
Vamos denotar por [tex]A[/tex] o evento "o apresentador abriu a porta [tex]3[/tex]".
Perceba que, inicialmente, o carro poderia estar atrás de qualquer porta; assim:
• [tex]P(C1)=P(C2)=P(C3)=\dfrac{1}{3}.[/tex]
As probabilidades de o apresentador abrir a porta [tex]3[/tex] em cada cenário são as seguintes:
• [tex] P(A|C1)=\dfrac{1}{2}[/tex] (Neste caso, o apresentador pode abrir a porta [tex]2[/tex] ou a [tex]3[/tex], ao acaso.);
• [tex] P(A|C2)=1[/tex] (Neste caso, o apresentador não pode abrir a porta [tex]2[/tex], logo ele tem que abrir a porta [tex]3[/tex].);
• [tex] P(A|C3)=0[/tex] (Neste caso, o apresentador não pode abrir a porta [tex]3[/tex], pois o carro está lá!).
Como escolhemos a porta [tex]1[/tex] e foi aberta a porta [tex]3[/tex], a probabilidade de ganharmos o carro com a troca é medida pela probabilidade condicional [tex]P(C2|A)[/tex].
Pelo Teorema de Bayes:
[tex]\,\\
\qquad P(C2|A)=\dfrac{P(C2)\cdot P(A|C2)}{P(C1)\cdot P(A|C1)+P(C2)\cdot P(A|C2)+P(C3)\cdot P(A|C3)}\\
\qquad P(C2|A)=\dfrac{\dfrac{1}{3}\cdot 1}{\,\dfrac{1}{3}\cdot \dfrac{1}{2}+\dfrac{1}{3}\cdot 1+\dfrac{1}{3}\cdot 0\,}\\
\qquad P(C2|A)=\dfrac{\dfrac{1}{3}}{\,\dfrac{1}{6}+\dfrac{1}{3}+0\,}\\
\qquad P(C2|A)=\dfrac{\dfrac{1}{3}}{\,\dfrac{3}{6}}=\dfrac{6}{\,9\,}\,\\
\qquad \boxed{P(C2|A)=\dfrac{2}{\,3\,}}\,.[/tex]
Para reforçar, podemos até calcular a probabilidade de perdermos o carro, se não fizermos a troca, utilizando o Teorema de Bayes. Essa probabilidade é a probabilidade condicional [tex]P(C1|A):[/tex]
[tex]\,\\
\qquad P(C1|A)=\dfrac{P(C1)\cdot P(A|C1)}{P(C1)\cdot P(A|C1)+P(C2)\cdot P(A|C2)+P(C3)\cdot P(A|C3)}\\
\qquad P(C1|A)=\dfrac{\dfrac{1}{3}\cdot \dfrac{1}{2}}{\,\dfrac{3}{6}\,}\\
\qquad P(C1|A)=\dfrac{\dfrac{1}{6}}{\,\dfrac{3}{6}}\,\\
\qquad \boxed{P(C1|A)=\dfrac{1}{\,3\,}}\,.[/tex]
Mais uma vez: a melhor opção é trocar a porta!
Importante: A probabilidade de ganhar só aumenta com a troca; mas isso não significa que vamos ganhar o carro fazendo a troca!
Um vídeo para ajudar…
Precisa de mais explicação?
Assista a este vídeo da série Isto é MATEMÁTICA.
É só clicar na telinha!
Monty Hall
Faça você mesmo!
Se, com todas essas explicações, você ainda acha que tanto faz manter ou trocar a porta inicialmente escolhida, é só fazer um teste prático a partir de, por exemplo, três copos descartáveis vazios e não transparentes.

De posse dos três copos, chame uma pessoa para fazer o papel do apresentador e siga os seguintes passos:
1) Peça para o "apresentador" esconder um objeto debaixo ou dentro de um dos copos, sem que você veja.
2) Escolha um dos copos e peça para o "apresentador" revelar um dos copos sem o objeto.
3) Troque a sua escolha inicial e peça para o "apresentador" revelar o copo com o objeto.
4) Anote o resultado.
5) Repita os passos anteriores umas [tex]50[/tex] vezes.
6) Faça as contas usando a razão:
[tex]\qquad \qquad \boxed{\dfrac{\text{ número de casos favoráveis }}{\text{número de casos possíveis}}}\,.[/tex]
Simulações
Não encontrou alguém para ajudar com a atividade "Faça você mesmo"?
Então faça simulações utilizando o aplicativo abaixo.
1) Faça uma tabelinha para anotar os resultados:
- Troca – carro ou bode;
- Não troca – carro ou bode.
2) Aguarde o aplicativo carregar.
3) Escolha uma porta e clique no quadradinho amarelo correspondente.
4) Clique no retângulo que irá aparecer, para que o apresentador abra uma porta.
5) Faça uma segunda escolha, mantendo ou trocando a porta inicialmente escolhida, e clique no quadradinho verde correspondente.
6) Anote o resultado.
7) Clique em Novo Jogo.
8) Repita os passos 3, 4, 5, 6 e 7 umas [tex]50[/tex] vezes.
9) Faça as contas usando a razão:
[tex]\qquad \qquad \boxed{\dfrac{\text{ número de casos favoráveis }}{\text{número de casos possíveis}}}\,.[/tex]
OBMEP_srg, criado com o GeoGebra
Adaptado de Mixedmoss
Um vídeo para encerrar…
Quebrando a banca
Voltar para Sala sobre probabilidade condicional
