Problema
(Indicado a partir do 9º ano do E. F.)
A figura a seguir mostra dois hexágonos regulares [tex]ABCDEF[/tex] e [tex]BGHICJ[/tex] com dois vértices coincidentes.
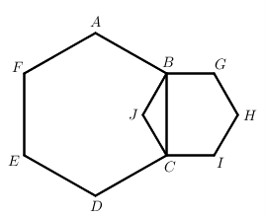
O hexágono menor tem área igual a [tex]\dfrac{3\sqrt{3}}{2}\;\text{cm}^2.[/tex]
Qual a área do hexágono maior?
Adaptado de PSS para professor substituto SEMEC – Teresina.
Ajudas
(1) Um triângulo equilátero de lado medindo [tex]l\text{ cm}[/tex] tem altura dada por [tex]h = \dfrac{l\sqrt{3}}{2}\text{ cm}[/tex] e área dada por [tex]A = \dfrac{l^2\sqrt{3}}{4} \text{ cm}^2.[/tex]
(2) Dado um hexágono regular de lado medindo [tex]l \text{ cm}[/tex], este pode ser dividido em seis triângulos equiláteros de lado medindo [tex]l \text{ cm}.[/tex]
OBMEP_srg, criado com o GeoGebra
Solução
Seja [tex]l[/tex] a medida em centímetros do lado do menor hexágono. Pela Ajuda 2, esse hexágono pode ser dividido em seis triângulos equiláteros de lado [tex]l[/tex].
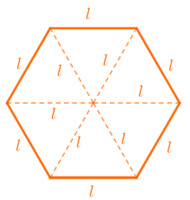
Como a área do menor hexágono é [tex]\dfrac{3\sqrt{3}}{2}\text{ cm}^2[/tex], então a área [tex]A_t[/tex] de cada um desses triângulos é dada por:
[tex]\quad A_t=\dfrac{\frac{3\sqrt{3}}{2}}{6} \\
\quad A_t= \dfrac{\sqrt{3}}{4} \text{ cm}^2.[/tex]
Mas, pela Ajuda 1, a área de um triângulo equilátero de lado medindo [tex]l\text{ cm}[/tex] é [tex]\dfrac{l^2\sqrt{3}}{4} \;\text{cm}^2[/tex]; assim, em particular, [tex]A_t=\dfrac{l^2\sqrt{3}}{4}[/tex] e, portanto, segue que:
[tex]\qquad \dfrac{l^2\sqrt{3}}{4} = \dfrac{\sqrt{3}}{4}\\
\qquad l^2 = 1\\
\qquad l = 1. [/tex]
Assim, a medida [tex]l[/tex] do lado do menor hexágono é [tex]l=1 \text{ cm}[/tex].
Novamente pela Ajuda 1, a altura [tex]h[/tex] de cada um desses triângulos equiláteros é dada por:
[tex]\qquad h = \dfrac{l\sqrt{3}}{2} = \dfrac{\sqrt{3}}{2} \text{ cm}[/tex].
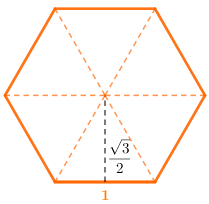
Agora precisamos encontrar a medida do lado do maior hexágono. Para isso, observe a figura abaixo, onde [tex]O[/tex] é o centro do hexágono [tex]BGHICJ[/tex] e perceba que a Ajuda 2 garante que esse hexágono também pode ser dividido em seis triângulos equiláteros.
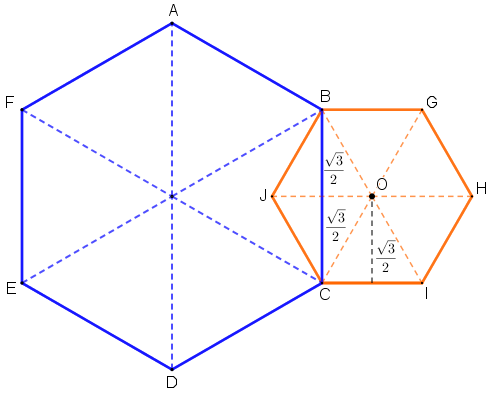
Note que o lado [tex]BC[/tex] do maior hexágono é igual à soma das alturas dos triângulos equiláteros [tex]BOJ[/tex] e [tex]COJ[/tex] e como estes são iguais, sendo [tex]L[/tex] a medida do lado do maior hexágono, temos
[tex]\qquad L = 2h\\
\qquad L = 2\dfrac{\sqrt{3}}{2}\\
\qquad L = \sqrt{3}\text{ cm}. [/tex]
Com isso, utilizando uma vez mais a Ajuda 1, temos que a área [tex]A_T[/tex] de cada um dos triângulos equiláteros que compõem o hexágono maior é dada por:
[tex]\qquad A_T=\dfrac{(\sqrt{3})^2\sqrt{3}}{4}=\dfrac{3\,\sqrt{3}}{4} \text{ cm}^2.[/tex]
Logo, sendo [tex]A[/tex] a área do maior hexágono, temos
[tex]\qquad A = 6\cdot \left(\dfrac{3\sqrt{3}}{4}\right)\\
\qquad \fcolorbox{black}{#eee0e5}{$A = \dfrac{9\sqrt{3}}{2}\text{ cm}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
