Problema
(Indicado a partir do 1º ano do E. M.)
Considere um triângulo retângulo [tex]ABC[/tex] de catetos [tex]\overline{BC}[/tex] e [tex]\overline{AC}[/tex] e hipotenusa [tex]\overline{BA}[/tex], cujas medidas são [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex], respectivamente.
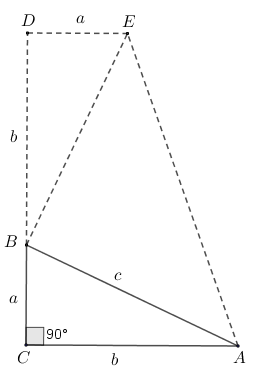
Prove o Teorema de Pitágoras, [tex]c^{2}=a^{2} + b^{2}[/tex], considerando que [tex]ACDE[/tex] é um trapézio.
(GERONIMO, J.R; FRANCO, V.S, Geometria Plana e Espacial: um estudo axiomático, 2ed, EDUEM, Maringá, PR, 2010)

Notações
✐ Denotaremos por [tex]A(T)[/tex] a área de uma região [tex]T[/tex] contida em um plano.
✐ Denotaremos por [tex]\triangle(ABC)[/tex] o triângulo de vértices [tex]A,B[/tex] e [tex]C[/tex].
✐ Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]\overline{AB}[/tex] e o seu comprimento por [tex]AB[/tex].
✐ Denotaremos por [tex] A\widehat{C}B[/tex] a medida do ângulo determinado pelo vértice [tex]C[/tex] e pelas semirretas definidas pelos segmentos [tex]\overline{CA} [/tex] e [tex]\overline{CB}[/tex].
Solução
Considere o triângulo [tex] ABC[/tex] da figura. De acordo com a construção do trapézio [tex]DEAC[/tex], a partir do triângulo [tex]ABC[/tex], temos que os segmentos [tex]\overline{DE}[/tex] e [tex]\overline{AC}[/tex] são paralelos.
Denotaremos por [tex]\textcolor{#FF6600}{T_1}[/tex], [tex]\textcolor{#0000FF}{T_2}[/tex] e [tex]\textcolor{#FF00FF}{T_3}[/tex] as regiões definidas pelos triângulos [tex]\triangle(DEB)[/tex], [tex]\triangle(EBA)[/tex] e [tex]\triangle(ABC)[/tex], respectivamente.
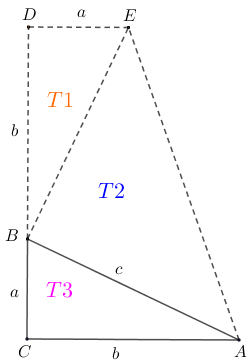
Observe que, por construção, temos que:
- [tex] B\widehat{C}A= B\widehat{D}E= 90^ {\circ}[/tex];[tex] \qquad \textcolor{#800000}{(i)}[/tex]
- [tex] D\widehat{E}B= C\widehat{B}A[/tex] e [tex] E\widehat{B}D= C\widehat{A}B[/tex];[tex] \qquad \textcolor{#800000}{(ii)}[/tex]
- [tex] E\widehat{B}D + D\widehat{E}B = 90^ {\circ} [/tex];[tex] \qquad \textcolor{#800000}{(iii)}[/tex]
- [tex] BE=c [/tex];[tex] \qquad \textcolor{#800000}{(iv)}[/tex]
e de [tex]\textcolor{#800000}{(i)}[/tex], [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], segue que:
[tex]\qquad E\widehat{B}A= 180^ {\circ} – (E\widehat{B}D + A\widehat{B}C )\\
\qquad E\widehat{B}A= 180^ {\circ} – (E\widehat{B}D + D\widehat{E}B )\\
\qquad E\widehat{B}A=180^ {\circ}-90^ {\circ}=90^ {\circ}.[/tex]
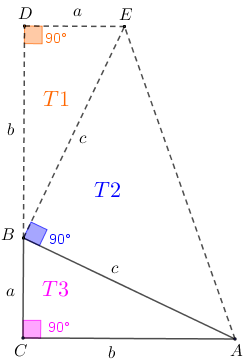
Note que os triângulos [tex]\triangle(BDE)[/tex], [tex]\triangle(EBA)[/tex] e [tex]\triangle(BCA)[/tex] são retângulos; assim, podemos encontrar as áreas das regiões [tex]\textcolor{#FF6600}{T_1}[/tex], [tex]\textcolor{#0000FF}{T_2}[/tex] e [tex]\textcolor{#FF00FF}{T_3}[/tex] utilizando os respectivos catetos dos triângulos como bases e alturas:
[tex]\qquad \textcolor{#FF6600}{A(T_{1})} = \dfrac{ab}{2}\\
\qquad \textcolor{#0000FF}{A(T_{2})}=\dfrac{c^{2}}{2}\\
\qquad \textcolor{#FF00FF}{A(T_{3})} = \dfrac{ab}{2}\,.[/tex]
Com isso, podemos calcular a área do trapézio [tex]DEAC[/tex]:
[tex]\qquad A(DEAC) =\textcolor{#FF6600}{A(T_{1})} + \textcolor{#0000FF}{A(T_{2})} +\textcolor{#FF00FF}{A(T_{3})}\\
\qquad A(DEAC)= \dfrac{ab}{2} + \dfrac{c^{2}}{2}+ \dfrac{ab}{2}\\
\qquad A(DEAC)=\dfrac{2ab+c^2}{2} \qquad \textcolor{#800000}{(v)}.[/tex]
Mas, por outro lado,
[tex]\qquad A(DEAC)=\dfrac{\left(\text{base maior}+\text{base menor}\right)\times \text{ altura}}{2} \\
\qquad A(DEAC)=\dfrac{(AC+ DE) \cdot DC}{2}\\
\qquad A(DEAC) = \dfrac{(b+a)(a+b)}{2}\\
\qquad A(DEAC) = \dfrac{a^{2} + 2ab + b^{2}}{2} \qquad \textcolor{#800000}{(vi)}.[/tex].
Portanto, comparando [tex]\textcolor{#800000}{(v)}[/tex] e [tex]\textcolor{#800000}{(vi)}[/tex], temos que:
[tex]\qquad \dfrac{2ab+c^2}{2}=\dfrac{a^{2} + 2ab + b^{2}}{2}\\
\qquad \dfrac{2ab+c^2}{\cancel{2}}=\dfrac{a^{2} + 2ab + b^{2}}{\cancel{2}}\\
\qquad 2ab+c^2=a^2 + 2ab + b^2\\
\qquad \cancel{2ab}+c^2=a^2 +\cancel{2ab}+ b^2\\
\qquad \fcolorbox{black}{#eee0e5}{$c^{2} = a^{2} + b^{2}$}\,;[/tex]
que é o que queríamos provar.
Solução elaborada pelos Moderadores do Blog.
