Problema
(Indicado a partir do 2º ano do E. M.)
(USAMTS, 2007-2008- Adaptado) Considere [tex]A[/tex] o conjunto formado pelos números naturais de [tex]1~[/tex] a [tex]~2n[/tex]:
- [tex]A=\{1,2,3, \cdots ,2n \}[/tex], com [tex]n \in \mathbb{N}.[/tex]
Ao eliminarmos [tex]n[/tex] números consecutivos de [tex]A[/tex], a soma dos números restantes é [tex]1615[/tex].
Encontre todos os valores possíveis de [tex]n[/tex].

Ajuda
[tex]\textcolor{#800000}{(1)}[/tex] A soma dos [tex]t[/tex] primeiros números naturais não nulos é dada por
[tex]\qquad \qquad \boxed{1+2+3+ \cdots+t=\dfrac{(t+1)\cdot t}{2}}[/tex]. (Se precisar, visite esta página.)
[tex]\textcolor{#800000}{(2)}[/tex] As raízes da equação do segundo grau [tex]~~ax^2+bx+c = 0~~[/tex] são dadas por
[tex]~~~~~~~~~~~~x_1 = \dfrac{-b+\sqrt{\Delta}}{2a}~~~[/tex] e [tex]~~~x_2 = \dfrac{-b-\sqrt{\Delta}}{2a}[/tex],
onde [tex]a,b,c[/tex] são números reais, com [tex]a\ne 0~[/tex], e [tex]~\Delta =b^2-4ac[/tex].
Solução
Vamos imaginar os números [tex]1\, ,\,2\, , \, 3\,, \, \dots\, , \, 2n[/tex] enfileirados ordenadamente. Retiraremos da fila [tex]n[/tex] números consecutivos.
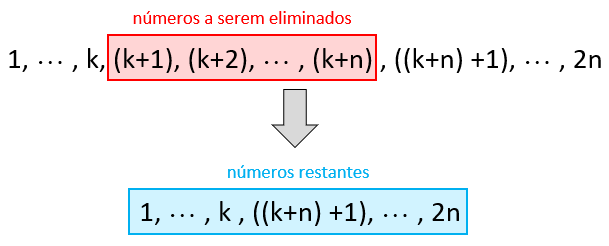
► Observe inicialmente que:
- quanto mais à esquerda da fila estiverem os números que retiraremos, maior será a soma dos remanescentes (vão sobrar os maiores);
- quanto mais à direita da fila estiverem os números que retiraremos, menor será a soma dos remanescentes (vão sobrar os menores).
Dessa forma,
- a menor soma possível para os números remanescentes acontecerá quando eliminarmos os [tex]n[/tex] últimos números;
- a maior soma possível para os números remanescentes acontecerá quando eliminarmos os [tex]n[/tex] primeiros números.
Vamos calcular essas duas somas e analisá-las usando a hipótese de que a soma dos números remanescentes deve ser [tex]1615[/tex] e, assim, a soma [tex]1615[/tex] não pode ser "menor do que a menor soma possível" e nem "maior do que a maior soma possível".
[tex]\qquad 1+2+3+\dots+n=\dfrac{(n+1)\cdot n}{2}=\dfrac{n^2+n}{2}.[/tex]

Assim, como a soma dos números remanescentes deve ser [tex]1615[/tex], particularmente [tex]\dfrac{n^2+n}{2} \leqslant 1615[/tex], ou seja, [tex] \boxed{n^2+n \leqslant 3230}.[/tex]
Para resolvermos a desigualdade [tex] \boxed{n^2+n \leqslant 3230}[/tex], poderíamos fazer o estudo da variação de sinal da expressão [tex] n^2+n -3230[/tex]; mas vamos tomar um caminho mais curto, observando que [tex] \sqrt{3230} \approx 56,8.[/tex]
Como [tex]56^2+56=3192\leqslant 3230\,[/tex], [tex]\,57^2+57=3606 \geqslant 3230\,[/tex] e [tex]n[/tex] é um número natural, podemos concluir que [tex]~\fcolorbox{black}{#e8e8e8}{$n \leqslant 56$}\,.[/tex]
[tex]\textcolor{#800000}{(ii)}[/tex] A soma máxima é dada por:
[tex]\qquad \begin{align*}(n+1)+(n+2)+\dots +(2n)&=(n+1)+(n+2)+\dots +(n+n)\\
&=(\underbrace {n+\dots+ n}_{n\text{ vezes}})+(1+2+\dots+n)\\
&=n^2+\dfrac{n^2+n}{2}=\dfrac{3n^2+n}{2}
\end{align*}[/tex]

Como a soma dos números remanescentes deve ser [tex]1615[/tex], particularmente [tex]\dfrac{3n^2+n}{2} \geqslant 1615[/tex], ou seja, [tex] \boxed{3n^2+n \geqslant 3230}.[/tex]
Aqui, para resolvermos a desigualdade [tex] \boxed{3n^2+n \geqslant 3230}[/tex], faremos o estudo da variação de sinal da expressão [tex] \boxed{3n^2+n -3230}.[/tex] Para isso, vamos observar o gráfico da função quadrática [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x)=3x^2+x -3230[/tex], que sabemos ser uma parábola, e responder a seguinte pergunta:
- Para que valores de [tex]x[/tex] temos [tex]f(x)\geqslant 0[/tex]?
Para traçar o gráfico de [tex]\, f[/tex] e analisar a variação de sinal, vamos precisar das raízes da equação de segundo grau [tex]3x^2+x -3230=0.[/tex] São elas:
[tex]\qquad x=\dfrac{-1\pm\sqrt{1^2-4\cdot 3\cdot (-3230)}}{6}\\
\qquad x=\dfrac{-1\pm\sqrt{38761}}{6} \\
\qquad x_1\dfrac{-1-\sqrt{38761}}{6} \approx -32,98 \qquad \text{e}\qquad x_2=\dfrac{-1+\sqrt{38761}}{6}\approx 32,65 [/tex]
Na imagem a seguir, à esquerda, vemos parte do gráfico de [tex]f[/tex]. À direita, vemos o mesmo gráfico com uma ampliação do eixo [tex]Ox[/tex], destacando os valores de [tex]x[/tex] para os quais [tex]f(x)\geqslant 0.[/tex]
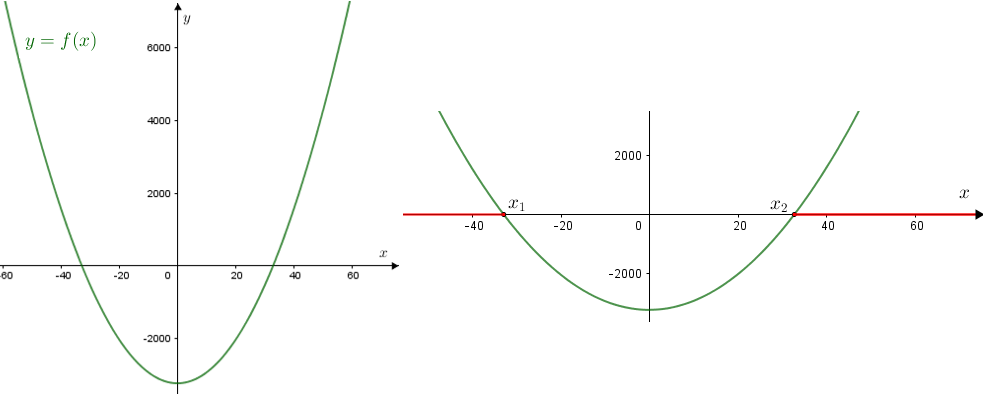
Lembre-se de que [tex]n[/tex] é um número natural; assim, os valores de [tex]x[/tex] que nos interessam são os números naturais não nulos do intervalo [tex][x_2,+\infty[.[/tex] Assim, [tex]~\fcolorbox{black}{#e8e8e8}{$n \geqslant 33$}\,.[/tex]
Portanto, utilizando o fato de a soma [tex]1615[/tex] não pode ser "menor do que a menor soma possível" e nem "maior do que a maior soma possível", concluímos que:
[tex]\fcolorbox{black}{#e8e8e8}{$33 \leqslant n \leqslant 56$}\,.\qquad \qquad \textcolor{#800000}{(iii)}[/tex]
► Agora, vamos voltar à situação geral do problema e supor que, dos [tex]n[/tex] números removidos, [tex]k+1[/tex] seja o primeiro.

Assim, segue que:
[tex]\qquad 1615=\left(1+2+\cdots+2n\right)-\left[(k+1)+(k+2)+\cdots+(k+n)\right]\\
\qquad 1615=\dfrac{(2n+1)\cdot 2n}{2}-\left[k \cdot n+(1+2+\cdots +n)\right]\\
\qquad 1615=\dfrac{(2n+1)\cdot 2n}{2}-\left[k \cdot n+\dfrac{(n+1)\cdot n}{2}\right]\\
\qquad 1615=\dfrac{(2n+1)\cdot 2n}{2}-\left[\dfrac{2k \cdot n+(n+1)\cdot n}{2}\right]\\
\qquad 3230=\left[(2n+1)\cdot 2n\right]-\left[2k \cdot n+(n+1)\cdot n \right]\\
\qquad 3230=(2n+1)\cdot 2n- n \cdot \left[2k +(n+1)\right]\\
\qquad \dfrac{3230}{n}=(2n+1)\cdot 2- \left(2k +n+1\right)\\
\qquad \dfrac{3230}{n}=4n+2-2k-n-1\\
\qquad \dfrac{3230}{n}=3n-2k+1.\qquad \qquad \textcolor{#800000}{(iv)}[/tex]
Note que [tex]3n-2k+1[/tex] é um número inteiro, assim, de [tex]\textcolor{#800000}{(iv)}[/tex], podemos concluir que [tex] \dfrac{3230}{n}[/tex] é também um número inteiro (mais especificamente, um número natural). Dessa forma, [tex]n[/tex] é um divisor positivo de [tex]3230[/tex]; vamos, então, determinar quais são esses divisores e, para isso, faremos a decomposição de [tex]3230[/tex] em fatores primos e, a partir dela, determinaremos todos os divisores positivos de [tex]3230[/tex].
|
[tex]\begin{array}{r|l} 3230& 2 \\1615 & 5 \\323& 17 \\19 & 19 \\1 \end{array}[/tex] |
[tex]\begin{array}{c} \hspace{1.4 cm} \end{array} \begin{array}{l} \, \fcolorbox{black}{#C6E2FF}{1} \, \\ \hline \end{array}[/tex] |
Perceba que, dentre os divisores positivos de [tex]3230[/tex], destacados em azul, os que satisfazem as desigualdades [tex]\textcolor{#800000}{(iii)}[/tex] são o [tex]34[/tex] e o [tex]38.[/tex]
Finalmente, veja que, de [tex]\textcolor{#800000}{(iv)}[/tex]:
[tex] \qquad \dfrac{3230}{34}=3\cdot 34-2k+1\\ |

|
[tex] \qquad \dfrac{3230}{38}=3\cdot 38-2k+1\\ |

|
Por tudo o que foi exposto, são possíveis apenas dois valores para [tex]n[/tex]: [tex]\fcolorbox{black}{#eee0e5}{$n=34$}\, ; \, \fcolorbox{black}{#eee0e5}{$n=38$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
