Problema
Na multiplicação indicada abaixo, as letras [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex] representam algarismos diferentes.
Determine [tex]A+B+C+D[/tex].
Observação: Letras iguais representam algarismos iguais.
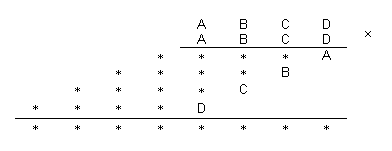
Solução 1
Observando a primeira linha da multiplicação, podemos perceber que o algarismo das unidades de [tex]D^2[/tex] é [tex]A[/tex].
Observando a quarta linha da multiplicação, notamos que o algarismo das unidades de [tex]D \cdot A[/tex] é [tex]D[/tex].
Assim, vamos analisar os possíveis casos :
[tex]\bullet \, \, D =0 \Rightarrow A=0[/tex]; (Este caso não é possível, pois [tex]A \ne D[/tex].)
[tex]\bullet \, \, D =1 \Rightarrow A=1[/tex]; (Este caso não é possível, pois [tex]A \ne D[/tex].)
[tex]\bullet \, \, D =2 \Rightarrow A=4 \Rightarrow A \cdot D = 8[/tex]; (Este caso não é possível, pois [tex] D \ne 8[/tex].)
[tex]\bullet \, \, D =3 \Rightarrow A=9 \Rightarrow A \cdot D = 27[/tex]; (Este caso não é possível, pois [tex]D \ne 7[/tex].)
[tex]\bullet \, \, D =4 \Rightarrow A=6 \Rightarrow A \cdot D = 24[/tex]; (Satisfaz, pois [tex] 4 = D[/tex].)
[tex]\bullet \, \, D =5 \Rightarrow A=5[/tex]; (Este caso não é possível, pois [tex]A \ne D[/tex].)
[tex]\bullet \, \, D =6 \Rightarrow A=6[/tex]; (Este caso não é possível, pois [tex]A \ne D[/tex].)
[tex]\bullet \, \, D =7 \Rightarrow A=9 \Rightarrow A \cdot D = 63[/tex]; (Este caso não é possível, pois [tex] D \ne 3[/tex].)
[tex]\bullet \, \, D =8 \Rightarrow A=4 \Rightarrow A \cdot D = 32[/tex]; (Este caso não é possível, pois [tex] D \ne 2[/tex].)
[tex]\bullet \, \, D =9 \Rightarrow A=1 [/tex]. (Este caso não é possível, pois se [tex]A=1, (ABCD)^2[/tex] teria menos de [tex]8[/tex] algarismos.)
Logo, [tex]A=6[/tex] e [tex]D=4[/tex].
Como [tex]D=4[/tex], da segunda e da terceira multiplicações temos as seguintes relações:
[tex]\bullet \, \, 4C[/tex] possui algarismo das unidades [tex]B[/tex].
[tex]\bullet \, \, 4B[/tex] possui algarismo das unidades [tex]C[/tex].
Vamos analisar os casos:
[tex]\bullet \, \, B=0 \Rightarrow D \cdot B = 4 \cdot 0 = 0 \Rightarrow C=0 \Rightarrow 4C = 0[/tex]; (Não satisfaz, pois teríamos [tex]B=C[/tex])
[tex]\bullet \, \, B=1 \Rightarrow D \cdot B = 4 \cdot 1 = 4\Rightarrow C=4 \Rightarrow 4C = 16[/tex]; (Não satisfaz, pois [tex]B\ne 6[/tex].)
[tex]\bullet \, \, B=2 \Rightarrow D \cdot B = 4 \cdot 2 = 8\Rightarrow C=8 \Rightarrow 4C = 32[/tex]; (Satisfaz!)
[tex]\bullet \, \, B=3 \Rightarrow D \cdot B = 4 \cdot 3 = 12\Rightarrow C=2 \Rightarrow 4C = 8[/tex]; (Não satisfaz, pois [tex]B\ne 8[/tex].)
[tex]\bullet \, \, B=5 \Rightarrow D \cdot B = 4 \cdot 5 = 20\Rightarrow C=0 \Rightarrow 4C = 0[/tex]; (Não satisfaz, pois [tex]B\ne 0[/tex].)
[tex]\bullet \, \, B=7 \Rightarrow D \cdot B = 4 \cdot 7 = 28\Rightarrow C=8 \Rightarrow 4C = 32[/tex]; (Não satisfaz, pois [tex]B\ne 2[/tex].)
[tex]\bullet \, \, B=8 \Rightarrow D \cdot B = 4 \cdot 8 = 32\Rightarrow C=2 \Rightarrow 4C = 8[/tex]; (Satisfaz!)
[tex]\bullet \, \, B=9 \Rightarrow D \cdot B = 4 \cdot 9 = 36\Rightarrow C=6 \Rightarrow 4C = 24[/tex]. (Não satisfaz, pois [tex]B\ne 4[/tex].)
Logo, os possíveis casos são [tex]B=2,C=8[/tex] ou [tex]B=8,C=2[/tex], e portanto [tex]A+B+C+D = 6+2+8+4=6+8+2+4 = 20[/tex].
Solução elaborada pelo aluno do PIC-OBMEP Angelo Donizeti Lorenconi Junior, com contribuições dos Moderadores do Blog.
Solução 2
Uma resolução para este problema vem da análise cuidadosa de um processo que fazemos quase que inconscientemente que é o algoritmo da multiplicação. Vamos tentar expor de maneira bem clara. Vejamos.
- ● Observe que, da indicação [tex]D \cdot D \rightarrow A[/tex], na primeira linha da multiplicação, e da indicação [tex] \, A \cdot D \rightarrow D[/tex], na quarta linha da multiplicação, podemos concluir, respectivamente, que:
[tex]\quad \rhd[/tex] o último algarismo de [tex]D \cdot D[/tex] é [tex]A[/tex], já que [tex]D \cdot D =\square A[/tex];[tex] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, (1)[/tex]
[tex]\quad\rhd[/tex] o último algarismo de [tex]A \cdot D[/tex] é [tex]D[/tex], já que [tex]A \cdot D =\square D[/tex];[tex] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, (2)[/tex]
onde, em cada caso, [tex]\square[/tex] representa um algarismo.
Assim, o último algarismo de [tex]D^3[/tex] é [tex]D[/tex] e com isso eliminamos quatro possibilidades para [tex]D \, [/tex]: [tex] \, \, 2 \, \, \, ; \, \, \, 3 \, \, \, ; \, \, \, 7 \, \, \, ; \, \, \, 8[/tex].
● Por outro lado, se [tex]D=0[/tex] ou [tex]D=1[/tex] ou [tex]D=5[/tex] ou [tex]D=6[/tex], de [tex](1)[/tex], concluiríamos que [tex]A=D[/tex], o que contraria a hipótese de que [tex]A, B, C, D[/tex] são algarismos distintos.
● Se [tex]D=9[/tex], teríamos [tex]A=1[/tex], já que o último algarismo de [tex]D \cdot D[/tex] é [tex]A[/tex].
Mas se [tex]A=1[/tex], na quarta linha da multiplicação teríamos [tex]A\cdot D=D[/tex]; [tex]A\cdot C=C[/tex]; [tex]A\cdot B=B[/tex] e [tex]A\cdot A=A[/tex], ou seja, nessa linha deveriam aparecer apenas quatro algarismos e não cinco como está indicado.
Pelo exposto, temos uma única possibilidade para [tex]D[/tex], qual seja, [tex]\fcolorbox{black}{yellow}{D=4} \, [/tex].
Como, por (1) o último algarismo de [tex]D \cdot D[/tex] é [tex]A[/tex], então [tex]\fcolorbox{black}{LightSteelBlue}{A=6} \, [/tex].
Mas o que nos revelam a segunda e a terceira linhas da multiplicação?
- ● Observe que, da indicação [tex]C \cdot D \rightarrow B[/tex] (segunda linha) e da indicação [tex] \, B \cdot D \rightarrow C[/tex] (terceira linha), podemos concluir que:
[tex]\quad\rhd[/tex] [tex]B[/tex] é o último algarismo de [tex]C \cdot D[/tex], já que [tex]C \cdot D =\square B[/tex][tex][/tex];
[tex]\quad\rhd[/tex] [tex]C[/tex] é o último algarismo de [tex]B \cdot D[/tex], já que [tex]B \cdot D =\square C[/tex][tex][/tex].
Sendo [tex]D[/tex] par, então [tex]B[/tex] e [tex]C[/tex] são pares também, assim, analisemos os pares [tex]0, 2, 8[/tex] que, ainda, temos a nossa disposição:
- ●Se [tex]C=0[/tex], na segunda linha da multiplicação teríamos [tex]0\cdot D=0[/tex]; [tex]0\cdot C=0[/tex]; [tex]0\cdot B=0[/tex] e [tex]0\cdot A=0[/tex], ou seja, nessa linha deveriam aparecer apenas quatro algarismos (todos iguais a zero) e não cinco como está indicado.
●De maneira análoga, se [tex]B=0[/tex], na terceira linha da multiplicação teríamos [tex]0\cdot D=0[/tex]; [tex]0\cdot C=0[/tex]; [tex]0\cdot B=0[/tex] e [tex]0\cdot A=0[/tex], ou seja, nessa linha também deveriam aparecer apenas quatro algarismos (todos iguais a zero) e não cinco como está indicado.
Assim só serão possíveis duas situações: [tex]\fcolorbox{black}{Lavender}{B=2} \, [/tex] e [tex]\fcolorbox{black}{DarkKhaki}{C=8} \, [/tex] ou [tex]\fcolorbox{black}{Lavender}{B=8} \, [/tex] e [tex]\fcolorbox{black}{DarkKhaki}{C=2} \, [/tex].
Dessa forma, se entendermos que estamos fazendo a multiplicação do número [tex]n[/tex] de quatro algarismos, [tex]n=ABCD[/tex] por ele próprio temos duas possibilidades para o número [tex]n[/tex]: [tex]n=6284 \, \, [/tex] ou [tex] \, \, n=6824[/tex].
Para qualquer uma delas, a resposta do problema é [tex]A+B+C+D=6+2+8+4=6+8+2+4=20[/tex], ou seja, [tex]\fbox{A+B+C+D=20}.[/tex]
Solução elaborada pelos Moderadores do Blog.

