.Problema Olímpico – Nível B: Uma divisão

Problema

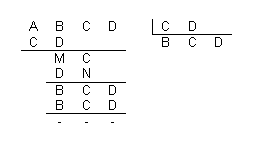
Determine [tex]A+B+C+D[/tex].
Observação: Letras iguais representam algarismos iguais.

Observação importante

Nas soluções abaixo, [tex]BCD[/tex] não significa [tex]B \times C \times D[/tex] e sim a notação decimal do número [tex]n=BCD[/tex], ou seja, [tex]n=B\times 10^2+C\times 10+D[/tex], como, por exemplo, em [tex]247=2\times 10^2+4\times 10+7[/tex].
Para entender melhor essa forma de representar números naturais, assista ao Vídeo 1 do PIC.

Solução 1

Observemos que:

• Da primeira divisão, temos que [tex]B\times C \, D=C \, D[/tex], o que nos leva a concluir que [tex]\boxed{B=1}[/tex].
• Da segunda divisão, temos que [tex]C\times C \, D=D \, N[/tex].
• Da terceira divisão, [tex]D\times C \, D=B \, C \, D[/tex] e, portanto, [tex]D^2=\square \, D[/tex], com [tex]\square[/tex] representando o algarismo das dezenas de [tex]D^2[/tex].
  Logo, temos duas possibilidades: [tex]D=5[/tex] ou [tex]D=6[/tex].

Como [tex]B\ne C[/tex], vamos, por tentativa, considerar [tex]C=2[/tex] e vejamos o que obtemos do produto [tex]D\times C \, D=B \, C \, D[/tex], considerando [tex]D=5[/tex] ou [tex]D=6[/tex]:
[tex]\bullet \quad 5\times 25=125[/tex], o que é válido, uma vez que [tex]B=1[/tex] e [tex]C=2[/tex], como estamos considerando;
[tex]\bullet \quad 6\times 26=156[/tex], o que não é válido, uma vez que [tex]C \ne 5[/tex].
 
Vejamos agora o que acontece, se considerarmos [tex]C=3[/tex]:
[tex]\bullet \quad 5\times 35=175[/tex], o que não é válido, uma vez que [tex]C\ne 7[/tex], como estamos considerando;
[tex]\bullet \quad 6\times 36=216[/tex], o que não é válido, uma vez que [tex]B\ne 2[/tex] e [tex]C \ne 1[/tex].
 
Observe que se considerarmos [tex]C\ge4[/tex], o produto [tex]C\times C \, D[/tex] não gerará dois dígitos, como indica a igualdade [tex]C\times C \, D=D \, N[/tex].
Assim temos que [tex]\boxed{D=5}[/tex] e [tex]\boxed{C=2}[/tex].
Por fim, para encontrar o valor de [tex]A[/tex], observemos que [tex]C \, D\times B \, C \, D=A \, B \, C \, D[/tex]. Logo, substituindo os valores encontrados para [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex] e efetuando a multiplicação [tex]C \, D\times B \, C \, D[/tex] obtemos:
[tex] \quad \quad 125 \\ \quad \times \, \, 25 \quad \\ \quad \overline{ \quad 3125 \quad }[/tex]
 
Portanto, [tex]\boxed{A=3}[/tex] e [tex]A+B+C+D=3+1+2+5=\boxed{\boxed{11}}[/tex].

Solução elaborada pelo aluno do PIC-OBMEP Giovani Heinzen Vicentin, com contribuições dos Moderadores do Blog.

Solução 2

♦ De [tex]B\times CD=CD[/tex] (primeira multiplicação), segue que [tex]\fcolorbox{black}{DarkSalmon}{B=1} \, [/tex], já que [tex]CD=0[/tex] não convém, pois não existe divisão por zero.
♦ Analisemos a última multiplicação.
Podemos reescrever [tex]D\times CD=BCD[/tex] como [tex]D\times CD=100\times B+CD[/tex], donde
[tex]\qquad (D\times CD)-(1\times CD)=100\times B[/tex],
ou ainda,
[tex]\qquad CD\times (D-1)=100\times B[/tex].
Como [tex]B=1[/tex], então [tex]CD\times (D-1)=100[/tex] e, portanto, o número [tex]CD[/tex] é um divisor positivo de [tex]100[/tex].
Observe que o número [tex]CD[/tex] tem dois dígitos; logo temos as seguintes possibilidades: [tex]\fbox{CD=10}[/tex]; [tex]\fbox{CD=20}[/tex], [tex]\fbox{CD=25}[/tex]; [tex]\fbox{CD=50}[/tex].
Mas se [tex]D=0[/tex], de [tex]CD\times (D-1)=100[/tex], teríamos que [tex]CD=-100[/tex]. Assim, necessariamente, [tex]CD=25[/tex] e, dessa forma, [tex]\fcolorbox{black}{PaleGoldenrod}{C=2} \, [/tex] e [tex]~\fcolorbox{black}{#FFBBFF}{D=5} \, [/tex].
♦ Finalmente, observe que a divisão é exata; logo [tex]BCD\times CD=ABDC[/tex].
Assim [tex]ABCD=125\times 25=3125[/tex], donde [tex]\fcolorbox{black}{#BBFFFF}{A=3} \, [/tex].
Pelo exposto, [tex]ABCD=3125[/tex] e [tex]\fbox{A+B+C+D=3+1+2+5=11} \, [/tex].

Solução elaborada pelos Moderadores do Blog.