Problema
(Indicado a partir do 9º ano do E. F.)
(XXXIX Olimpíada de Matemática Espanhola– 2003) Quais são as possibilidades para a medida da área de um hexágono que tem todos os ângulos internos com a mesma medida e cujos lados medem, em centímetros, [tex]1,2,3,4,5,6[/tex], não necessariamente nessa ordem?

Lembretes
(1) A soma dos ângulos internos de um polígono convexo de [tex]n[/tex] lados [tex](n\gt 2)[/tex] é dada por:
[tex]\qquad \qquad \boxed{S_{i_n}=\left(n-2\right)\cdot 180^\circ}.[/tex]
(2) Resista à tentação de pensar que se um polígono é equiângulo (tem todos os ângulos internos com a mesma medida), então ele necessariamente é equilátero (tem todos os lados com a mesma medida).(Por exemplo, um retângulo não quadrado é um polígono equiângulo, mas não equilátero.)
(3) A área de um triângulo equilátero de lados com comprimento [tex]x[/tex] é dada por:
[tex]\qquad A_{teq}=\dfrac{x^2\cdot\sqrt{3}}{4}.[/tex]
(Por falar em área de triângulo equilátero, visite esta Sala para leitura.)
Solução
Vamos resolver o problema utilizando ferramentas matemáticas nada complicadas. Ele foi colocado como um desafio, pois envolve um tipo de raciocínio não muito comum.
Este é um daqueles problemas que, depois de resolvido, não é nada difícil entendermos a sua solução. Na verdade, este é um típico problema olímpico. Vamos lá, tentaremos fazer uma solução bem explicadinha…
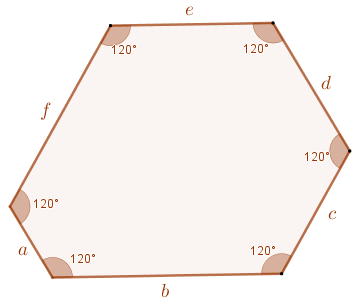
Sejam [tex]a,b,c,d,e\, [/tex] e [tex]\, f[/tex] os comprimentos dos lados do hexágono em questão.
Com isso,
[tex]\qquad \qquad a+b+c+d+e+f=1+2+3+4+5+6=21.[/tex]
Como esse hexágono tem todos os ângulos internos com a mesma medida, ele não pode ser côncavo. Sendo convexo, a soma dos ângulos internos desse hexágono é
[tex]\qquad \qquad S_{i_6}=\left(6-2\right)\cdot 180^\circ= 720^\circ[/tex]
e, portanto, cada um de seus ângulos internos mede [tex]\dfrac{720^\circ}{6}=120^\circ\, [/tex], conforme ilustra a figura ao lado.
Dessa forma, podemos prolongar os lados desse hexágono e formar um grande triângulo equilátero! (Este é o "pulo do gato"!)
- Com efeito, como os ângulos internos medem todos [tex]120^\circ\, [/tex], então seus respectivos suplementos medem [tex]60^\circ\, [/tex] e, portanto, definem três triângulos equiláteros pequenos. Isso faz com que o triângulo externo seja também equilátero, pois terá três ângulos de [tex]60^\circ\, [/tex].
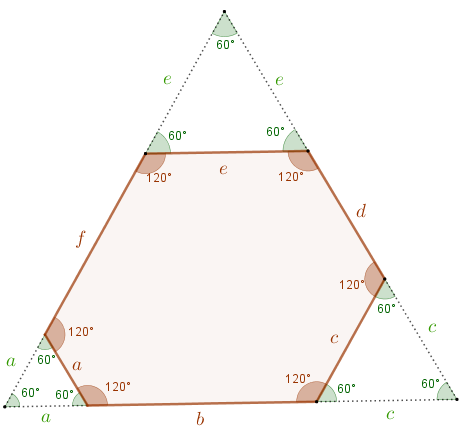
Seja, então, [tex]l[/tex] o comprimento de cada lado do triângulo externo que construímos. Assim, [tex]l = a + b + c = c + d + e = e + f + a[/tex] e, portanto:
[tex]\qquad (a + b + c)+(c + d + e)+( e + f + a)=3l[/tex]
[tex]\qquad (a + b + c+ d + e + f)+(a+c+e)=3l[/tex]
[tex]\qquad 21+(a+c+e)=3l[/tex]
[tex]\qquad \boxed{l=7+\dfrac{a+c+e}{3}}. \qquad \qquad \textcolor{#800000}{(i)}[/tex]
Como os lados do hexágono medem [tex]1,2,3,4,5[/tex] e [tex]6[/tex] centímetros, o menor valor que a soma [tex]a+c+e[/tex] pode assumir é [tex]1+2+3=6[/tex] e o maior é [tex]4+5+6=15[/tex]. Logo, temos que:
[tex]\qquad 2 \leqslant \dfrac{a+c+e}{3} \leqslant 5[/tex]
[tex]\qquad 7+ 2 \leqslant 7+\dfrac{a+c+e}{3} \leqslant 7+5[/tex]
[tex]\qquad 9 \leqslant 7+\dfrac{a+c+e}{3} \leqslant 12[/tex]
ou seja, [tex]9 \leqslant l \leqslant 12\, .[/tex]
Vamos ter que analisar cada um desses quatro casos; e em cada análise, para efeito dos cálculos que faremos, nos interessará especificamente as medidas dos lados dos três triângulos equiláteros menores.
Neste caso, por [tex]\textcolor{#800000}{(i)}[/tex], temos [tex]a+c+e=6[/tex].
Como [tex]a+b+c+d+e+f=21[/tex], segue que [tex]b+d+f=15[/tex]. Como a soma [tex]6[/tex] é a mínima possível e a soma [tex]15[/tex] é a máxima possível, então [tex]a,c,e \in \{1,2,3\}[/tex] e [tex]b,d,f,\in \{4,5,6\}[/tex]. Assim, os lados dos triângulos equiláteros menores medem [tex]1,\, 2\, [/tex] e [tex]\, 3[/tex] centímetros. Perceba que não importa a ordem em que escolhemos os valores de [tex]a,c,e[/tex], dentre os apresentados; pois para escolhas diferentes obteríamos o mesmo hexágono, apenas em uma posição diferente. Logo, sem perda de generalidade, podemos fazer:
- [tex]a=1;\, c=2;\, e=3[/tex].
Neste caso, por [tex]\textcolor{#800000}{(i)}[/tex], temos [tex]a+b+c=9[/tex]. Mais uma vez, como [tex]a+b+c+d+e+f=21[/tex], segue que [tex]d+e+f=12.[/tex]
Aqui as escolhas para os valores de [tex]a,b,c,d,e,f[/tex] serão um pouco mais complicadas.
A princípio, como os valores de [tex]a,c,e[/tex] são distintos, temos que [tex]a,c,e \in \{1,2,6\}[/tex], [tex]a,c,e \in \{1,3,5\}[/tex] ou [tex]a,c,e \in \{2,3,4\}.[/tex]
Dessa forma, aqui temos três possibilidades:
► [tex]a,c,e \in \{1,2,6\}\, [/tex] e [tex]\, b,d,f,\in \{3,4,5\}[/tex]
► [tex]a,c,e \in \{1,3,5\}\, [/tex] e [tex]\, b,d,f,\in \{2,4,6\}[/tex]
► [tex]a,c,e \in \{2,3,4\}\, [/tex]e [tex]\, b,d,f,\in \{1,5,6\}[/tex]
Assim, [tex]a,c,e \in \{1,3,5\}\, [/tex] e, sem perda de generalidade, podemos fazer:
- [tex]a=1;\, c=3;\, e=5.[/tex]
Neste caso, por [tex]\textcolor{#800000}{(i)}[/tex], temos [tex]a+c+e=12[/tex]. Mais uma vez, como [tex]a+b+c+d+e+f=21[/tex], segue que [tex]b+d+f=9.[/tex]
Aqui as escolhas para os valores de [tex]a,b,c,d,e,f[/tex] também não serão feitas diretamente.
Inicialmente, para os valores de [tex]a,c,e[/tex] teremos [tex]a,c,e \in \{1,5,6\}[/tex], [tex]a,c,e \in \{2,4,6\}[/tex] ou [tex]a,c,e \in \{3,4,5\}.[/tex]
Dessa forma, aqui temos três possibilidades:
► [tex]a,c,e \in \{1,5,6\}\, [/tex] e [tex]\, b,d,f,\in \{2,3,4\}[/tex]
► [tex]a,c,e \in \{2,4,6\}\, [/tex] e [tex]\, b,d,f,\in \{1,3,5\}[/tex]
► [tex]a,c,e \in \{3,4,5\}\, [/tex]e [tex]\, b,d,f,\in \{1,2,6\}[/tex]
Assim, [tex]a,c,e \in \{2,4,6\}\, [/tex] e,sem perda de generalidade, podemos fazer:
- [tex]a=2;\, c=4;\, e=6.[/tex]
Neste caso, por [tex]\textcolor{#800000}{(i)}[/tex], temos [tex]a+c+e=15.[/tex]
Como [tex]a+b+c+d+e+f=21[/tex], segue que [tex]b+d+f=6.[/tex] Como a soma [tex]6[/tex] é a mínima possível e a soma [tex]15[/tex] é a máxima possível, então [tex]a,c,e \in \{4,5,6\}[/tex] e [tex]b,d,f,\in \{1,2,3\}[/tex]. Sem perda de generalidade, podemos fazer:
- [tex]a=4;\, c=5;\, e=6.[/tex]
A partir dos quatro casos de comprimentos possíveis para os lados do hexágono, podemos finalmente calcular as possibilidades para a medida da sua área. Para tanto, observe que a medida da área do hexágono é a diferença entre a "medida da área do triângulo maior" e a "soma das medidas das áreas dos três triângulos menores ".
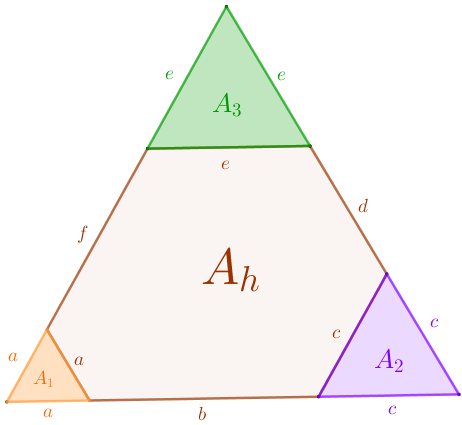
Assim, se [tex]A_t[/tex] é a medida da área do triângulo maior, então [tex]\boxed{\textcolor{#993300}{A_h}=A_t-\left(\textcolor{#ff6600}{A_1}+\textcolor{#7f00ff}{A_2}+\textcolor{#009900}{A_3} \right)}\, .[/tex] Utilizando a fórmula do Lembrete (3), segue que:
[tex]\qquad \qquad \textcolor{#993300}{A_h}=A_t-\left(\textcolor{#ff6600}{A_1}+\textcolor{#7f00ff}{A_2}+\textcolor{#009900}{A_3} \right)[/tex]
[tex]\qquad \qquad \textcolor{#993300}{A_h}=\dfrac{l^2\cdot\sqrt{3}}{4}-\left(\textcolor{#ff6600}{\dfrac{a^2\cdot\sqrt{3}}{4}}+\textcolor{#7f00ff}{\dfrac{c^2\cdot\sqrt{3}}{4}}+\textcolor{#009900}{\dfrac{e^2\cdot\sqrt{3}}{4}} \right)[/tex]
[tex]\qquad \qquad \textcolor{#993300}{A_h}=\dfrac{\sqrt{3}}{4} \cdot \left(l^2-\textcolor{#ff6600}{a^2}-\textcolor{#7f00ff}{c^2}-\textcolor{#009900}{e^2} \right).[/tex]
A tabela abaixo mostra os resultados dos cálculos da área do hexágono nos quatro casos possíveis analisados.
[tex] \begin{array}{c|c|c|c|c}
l& \textcolor{#ff6600}{a} & \textcolor{#7f00ff}{c} & \textcolor{#009900}{e} & \textcolor{#993300}{A_h}\\
\hline
9\, cm & \textcolor{#ff6600}{1\, cm} & \textcolor{#7f00ff}{2\, cm} & \textcolor{#009900}{3\, cm} & \textcolor{#993300}{\, \dfrac{67\sqrt{3}}{4}\, cm^2}\\
\hline
10\, cm & \textcolor{#ff6600}{1\, cm} & \textcolor{#7f00ff}{3\, cm} & \textcolor{#009900}{5\, cm} & \textcolor{#993300}{\, \dfrac{65\sqrt{3}}{4}\, cm^2}\\
\hline
11\, cm & \textcolor{#ff6600}{2\, cm} & \textcolor{#7f00ff}{4\, cm} & \textcolor{#009900}{6\, cm} & \textcolor{#993300}{\, \dfrac{65\sqrt{3}}{4}\, cm^2}\\
\hline
12\, cm & \textcolor{#ff6600}{4\, cm} & \textcolor{#7f00ff}{5\, cm} & \textcolor{#009900}{6\, cm} & \textcolor{#993300}{\, \dfrac{67\sqrt{3}}{4}\, cm^2}\\
\hline \end{array}[/tex]
Solução elaborada pelos Moderadores do Blog.
