Problema
(Indicado a partir do 1º ano do E. M.)
(UERJ– Adaptado) Um skatista treina em três rampas planas de mesmo comprimento [tex]a[/tex], mas com inclinações diferentes. As figuras abaixo representam as rampas.
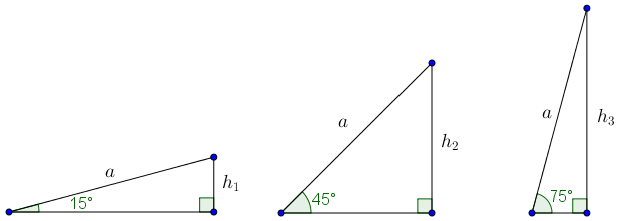
Sabendo que as alturas, em metros, das rampas são [tex]h_{1}[/tex], [tex]h_{2}[/tex] e [tex]h_{3}[/tex], encontre o valor de [tex]h_{1} +h_{2}[/tex] em função de [tex]h_{3}[/tex].
Solução 1
Inicialmente, notem que o primeiro e terceiro triângulos são congruentes e que o triângulo do meio é isósceles.
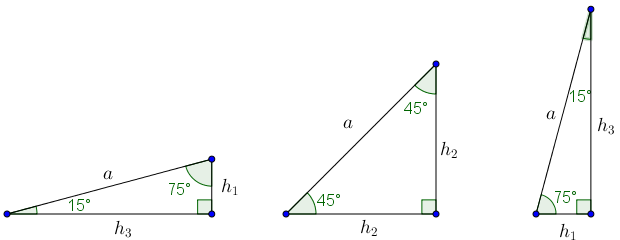
Vamos desenhar os dois últimos triângulos com o vértice [tex]A[/tex] em comum e com as bases de comprimentos [tex]h_{1}[/tex] e [tex]h_{2}[/tex] colineares.
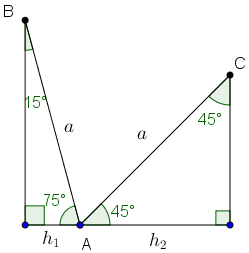
Note que o ângulo [tex]B\hat{A}C[/tex] mede [tex]180^\circ-45^\circ-75^\circ=\boxed{60^\circ}[/tex] e que, ao construirmos o segmento [tex]\overline{BC}[/tex], obtemos o triângulo [tex]ABC[/tex] que é isósceles e tem um ângulo de [tex]60^\circ[/tex]. Portanto, o triângulo [tex]ABC[/tex] é equilátero com lados com comprimento [tex]a[/tex].
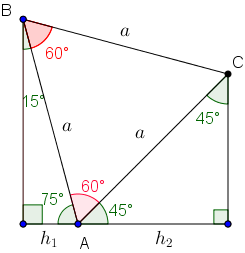
Agora, construindo o segmento [tex]\overline{CD}[/tex] paralelo às bases [tex]h_{1}[/tex] e [tex]h_{2}[/tex], obtemos o triângulo retângulo [tex]BDC[/tex] com hipotenusa [tex]a[/tex] e ângulos [tex]60^\circ + 15^\circ=\boxed{75^\circ}[/tex], [tex]\boxed{90^\circ}[/tex] e [tex]\boxed{15^\circ} \, .[/tex] Portanto, o triângulo [tex]BDC[/tex] é congruente ao triângulo da primeira rampa, pelo caso de congruência A.L.A..
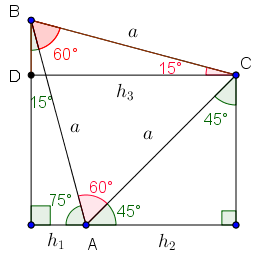
Logo, pela última construção, [tex]\boxed{h_{3}=h_{1}+h_{2}} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembretes para a Solução 2
(1) [tex]sen \, (\alpha + \beta) = sen \, \alpha \cdot cos \, \beta + sen \, \beta \cdot cos \, \alpha[/tex]
(2) [tex]sen \, (\alpha-\beta) = sen \, \alpha \cdot cos\beta – sen \, \beta \cdot cos \, \alpha[/tex]
(3) Ângulos especiais e seus senos e cossenos:
[tex] \, \, sen \, 30^{\circ}=\dfrac{1}{2};\qquad cos \, 30^{\circ}=\dfrac{\sqrt{3}}{2}[/tex][tex]; \qquad sen \, 45^{\circ}=\dfrac{\sqrt{2}}{2}; \qquad[/tex] [tex] cos \, 45^{\circ}=\dfrac{\sqrt{2}}{2}[/tex].
Solução 2
Podemos utilizar Trigonometria para resolver o problema; vejamos.
Observando o primeiro triângulo, podemos concluir que:
[tex]\qquad \qquad sen \, 15 ^\circ= \dfrac{h_{1}}{a}\\
\qquad \qquad h_{1} = a \cdot sen \, 15 ^\circ[/tex]
De modo análogo, observando os outros dois triângulos, obtemos que:
|
[tex]\qquad sen \, 45 ^\circ= \dfrac{h_{2}}{a} \\ \qquad h_{2} = a \cdot sen \, 45 ^\circ[/tex] |
[tex]\qquad sen \, 75 ^\circ= \dfrac{h_{3}}{a} \\ \qquad h_{3} = a \cdot sen \, 75 ^\circ[/tex] |
Pelo Lembrete (1) :
[tex]\qquad sen \, 75 ^\circ = sen \, (45 ^\circ + 30 ^\circ) = sen \, 45 ^\circ \cdot cos 30 ^\circ + sen \, 30 ^\circ \cdot cos 45 ^\circ\\
\qquad sen \, 75 ^\circ = \dfrac {\sqrt{2}}{2} \cdot \dfrac {\sqrt{3}}{2} + \dfrac {1}{2} \cdot \dfrac {\sqrt{2}}{2} = \dfrac {\sqrt{6}+\sqrt{2}}{4}.[/tex]
Pelo Lembrete (2) :
[tex]\qquad sen \, 15 ^\circ = sen \, (45 ^\circ – 30 ^\circ) = sen \, 45 ^\circ \cdot cos 30 ^\circ – sen \, 30 ^\circ \cdot cos 45 ^\circ \\
\qquad sen \, 15 ^\circ= \dfrac {\sqrt{2}}{2} \cdot \dfrac {\sqrt{3}}{2} – \dfrac {1}{2} \cdot \dfrac {\sqrt{2}}{2} = \dfrac {\sqrt{6}-\sqrt{2}}{4}.[/tex]
Portanto:
[tex]\qquad h_{1} = a \cdot sen \, 15 ^\circ = a \cdot\left(\dfrac {\sqrt{6}-\sqrt{2}}{4}\right)[/tex];
[tex]\qquad h_{2} = a \cdot sen \, 45 ^\circ = a \cdot \dfrac {\sqrt{2}}{2}[/tex];
[tex]\qquad h_{3} = a \cdot sen \, 75 ^\circ = a \cdot \left(\dfrac {\sqrt{6}+\sqrt{2}}{4}\right)[/tex].
Somando [tex]h_{1}[/tex] e [tex]h_{2}[/tex], temos que:
[tex]\qquad \begin{align*}\boxed{h_{1} + h_{2}} &= a \cdot \left(\dfrac {\sqrt{6}-\sqrt{2}}{4}\right) +a \cdot \dfrac {\sqrt{2}}{2}\\
& = a \cdot\left(\dfrac {\sqrt{6}-\sqrt{2}}{4}+\dfrac {\sqrt{2}}{2}\right)\\
& = a \cdot \left(\dfrac {\sqrt{6}+\sqrt{2}}{4}\right)\\
&=\boxed{h_{3}} \, .\end{align*}[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembretes para a Solução 3
(4) [tex] \, \, sen \, 30^{\circ}=\dfrac{1}{2}[/tex].
(5) [tex]sen \, \alpha +sen \, \beta =2 \cdot sen \, \left(\dfrac{\alpha+\beta}{2}\right) \cdot cos \, \left( \dfrac{\alpha-\beta}{2}\right) [/tex]
Solução 3
Vamos fazer mais uma solução utilizando Trigonometria!
Do primeiro triângulo, podemos concluir que:
[tex]\qquad sen \, 15 ^\circ= \dfrac{h_{1}}{a} \\
\qquad h_{1} = a \cdot sen \, 15 ^\circ \, .[/tex]
De modo análogo, dos outros dois triângulos, obtemos que:
|
[tex]\qquad sen \, 45 ^\circ= \dfrac{h_{2}}{a} \\ \qquad h_{2} = a \cdot sen \, 45 ^\circ[/tex] |
[tex]\qquad sen \, 75 ^\circ= \dfrac{h_{3}}{a} \\ \qquad h_{3} = a \cdot sen \, 75 ^\circ[/tex] |
Pelo Lembrete (5) :
[tex]\qquad sen \, 45^\circ +sen \, 15^\circ =2 \cdot sen \, \left( \dfrac{45^\circ+15^\circ}{2}\right) \cdot cos\left( \dfrac{45^\circ-15^\circ}{2}\right) [/tex]
[tex]\qquad sen \, 45^\circ +sen \, 15^\circ =2 \cdot sen \, 30^\circ \cdot cos \, 15^\circ. \qquad \qquad \textcolor{#800000}{(i)}[/tex]
Mas ângulos com medidas [tex] \, 15 ^\circ \text{ e }75 ^\circ[/tex] são complementares, logo [tex]cos \, 15 ^\circ = sen \, 75 ^\circ[/tex]. Assim, podemos reescrever a igualdade [tex]\textcolor{#800000}{(i)}[/tex] da seguinte forma:
[tex]\qquad sen \, 45^\circ +sen \, 15^\circ =2 \cdot sen \, 30^\circ \cdot sen \, 75^\circ. \qquad \qquad \textcolor{#800000}{(ii)} [/tex]
Com isso, segue que:
[tex]\qquad h_{1} +h_{2}[/tex]=[tex]a \cdot sen \, 15 ^\circ+ a \cdot sen \, 45 ^\circ[/tex]
[tex]\qquad h_{1} +h_{2}[/tex]=[tex]a \cdot( sen \, 15 ^\circ+ sen \, 45 ^\circ)[/tex]
[tex]\qquad h_{1} +h_{2}\stackrel{\textcolor{#800000}{(ii)}}{=}a \cdot( 2 \cdot sen \, 30^\circ \cdot sen \, 75^\circ)[/tex]
[tex]\qquad h_{1} +h_{2}[/tex]=[tex]a \cdot( \cancel{2} \cdot \dfrac{1}{\cancel{2}} \cdot sen \, 75 ^\circ)[/tex]
[tex]\qquad h_{1} +h_{2}[/tex]=[tex]a \cdot sen \, 75 ^\circ[/tex]
[tex]\qquad \boxed{h_{1}+h_{2}=h_{3}} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
