Problema
(Indicado a partir do 3º ano do E. M.)
(Olimpíadas BULGÁRIA) Os comprimentos das alturas de um triângulo [tex]ABC[/tex] são as três soluções da equação cúbica [tex]\boxed{x^3+kx^2+ lx-m=0}[/tex].
Determine o raio do círculo inscrito no triângulo [tex] ABC[/tex].
 |
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex] Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex]. |
Solução
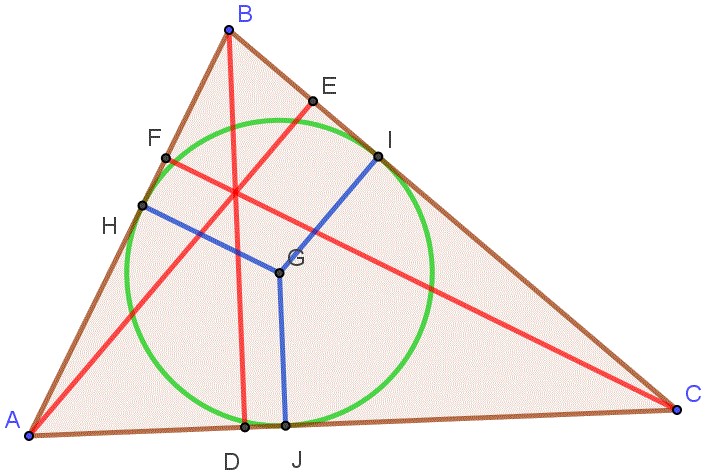
Sem perda de generalidade, podemos supor que o triângulo [tex]ABC[/tex] seja acutângulo, conforme mostrado na figura a seguir.
Na figura, estamos supondo que os segmentos [tex]\overline{AE}[/tex], [tex]\overline{BD}[/tex] e [tex]\overline{CF}[/tex] são as alturas do triângulo [tex]ABC[/tex] relativas, respectivamente, aos lados [tex]\overline{BC}[/tex], [tex]\overline{AC}[/tex] e [tex]\overline{AB}\, .[/tex]
Se considerarmos que [tex]x_1[/tex], [tex]x_2[/tex] e [tex]x_3[/tex] são as raízes da equação cúbica [tex]\boxed{x^3+kx^2+ lx-m=0}[/tex], utilizando as relações de Girard, obtemos que:
[tex]\qquad \textcolor{#800000}{(i)}[/tex] [tex]x_1+x_2+x_3=-k [/tex];
[tex]\qquad \textcolor{#800000}{(ii)}[/tex] [tex] x_1\cdot x_2+ x_1\cdot x_3+ x_2\cdot x_3=l [/tex];
[tex]\qquad \textcolor{#800000}{(iiii)}[/tex] [tex] x_1\cdot x_2\cdot x_3=m[/tex].
[tex]\textcolor{#800000}{(iv)}[/tex] Sem perda de generalidade, podemos considerar, em acordo com as informações do problema, que:
[tex]\qquad AE= x_1[/tex];
[tex]\qquad BD = x_2[/tex];
[tex]\qquad CF = x_3[/tex] .
Considerando a área [tex]S[/tex] do triângulo [tex]ABC[/tex], observe que podemos calculá-la das seguintes maneiras:
[tex]\qquad \textcolor{#800000}{(v)}[/tex] [tex] S = p\cdot r[/tex] , onde:
[tex]\qquad \qquad r[/tex] é o raio do círculo inscrito no triângulo [tex]ABC[/tex],
[tex]\qquad \qquad p[/tex] é o semiperímetro do triângulo [tex]ABC[/tex], ou seja, [tex]2p=AC+ BC+ AB\, .[/tex]
[tex]\qquad \textcolor{#800000}{(vi)}[/tex] [tex]S = \dfrac {(base) \cdot (altura)} {2}[/tex], podendo aqui considerar três situações possíveis, conforme a afirmação [tex]\textcolor{#800000}{(iv)}[/tex]:
[tex]\qquad \qquad \textcolor{#800000}{(1)}[/tex] [tex]S= \dfrac {x_1\cdot BC} {2}[/tex], donde [tex] BC= \dfrac {2S} {x_1}[/tex];
[tex]\qquad \qquad \textcolor{#800000}{(2)}[/tex] [tex]S= \dfrac {x_2\cdot AC} {2}[/tex], donde [tex] AC= \dfrac {2S} {x_2}[/tex];
[tex]\qquad \qquad \textcolor{#800000}{(3)}[/tex] [tex]S= \dfrac {x_3\cdot AB} {2}[/tex], donde [tex] AB= \dfrac {2S} {x_3}[/tex].
Somando as equações [tex]\textcolor{#800000}{(1)}[/tex], [tex]\textcolor{#800000}{(2)}[/tex] e [tex]\textcolor{#800000}{(3)}[/tex] de [tex]\textcolor{#800000}{(vi)}[/tex], obtemos:
[tex]\, \\
\qquad \underbrace{BC + AC + AB}_{perímetro=2p} = \dfrac {2S} {x_1}\ + \dfrac {2S} {x_2}\ + \dfrac {2S} {x_3}\\
\qquad \cancel{2}p\ = {\cancel{2}S}\cdot \left(\dfrac {1} {x_1}\ + \dfrac {1} {x_2}\ + \dfrac {1} {x_3}\right)\\
\qquad p\ = {S}\cdot \left(\dfrac {x_2\cdot x_3+ x_1\cdot x_3+ x_1\cdot x_2} {x_1\cdot x_2\cdot x_3}\right).[/tex]
Por [tex]\textcolor{#800000}{(v)}[/tex], concluímos que [tex] \dfrac {S} {r} = p [/tex] e, substituindo essa expressão na equação anterior, segue que:
[tex]\qquad \dfrac {\cancel{S}} {r} = {\cancel{S}}\cdot \left(\dfrac {x_2\cdot x_3+ x_1\cdot x_3+ x_1\cdot x_2} {x_1\cdot x_2\cdot x_3}\right)\\
\qquad \dfrac {1} {r} = \dfrac {x_2\cdot x_3+ x_1\cdot x_3+ x_1\cdot x_2} {x_1\cdot x_2\cdot x_3}\\
\qquad \dfrac {1} {r} = \dfrac {x_1\cdot x_2+ x_1\cdot x_3+ x_2\cdot x_3} {x_1\cdot x_2\cdot x_3}\\
\, [/tex]
Substituindo [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex] na equação acima:
[tex]\qquad \dfrac {1} {r} = \dfrac {l} {m}\\
\qquad r\ = \dfrac {m} {l}.\\
\, [/tex]
- Conclusão: O raio do círculo inscrito no triângulo[tex]ABC[/tex] é igual à razão [tex]\dfrac {m} {l}[/tex].
Solução elaborada pelos Moderadores do Blog.
