Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Seu Horácio tem duas escadas com o mesmo tamanho.
Ele apoiou cada uma delas na parte superior de dois muros paralelos, distantes [tex]5[/tex] metros um do outro, conforme ilustra a figura abaixo.
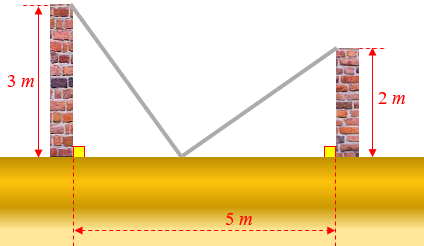
Sabendo que um dos muros tem altura [tex]2[/tex] metros e o outro [tex]3[/tex] metros, qual o comprimento das escadas?
Lembrete
Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução 1
Considere [tex]A, \, B, \, C, \, D[/tex] os pontos superiores e inferiores dos dois muros na vista lateral ilustrada na figura abaixo. Considere também na mesma vista lateral o ponto [tex]E[/tex] que corresponde ao encontro dos pés das duas escadas. Dessa forma, se [tex]c[/tex] é o comprimento em metros de cada escada, ficam definidos os triângulos retângulos [tex]ACE[/tex] e [tex]BDE[/tex] ilustrados na imagem a seguir.
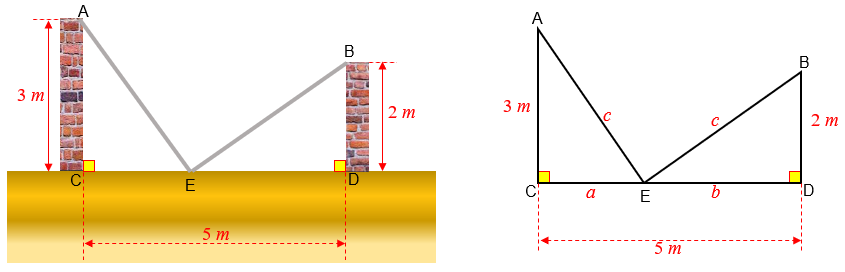
Aplicando o Teorema de Pitágoras aos triângulos retângulos [tex]ACE[/tex] e [tex]BDE[/tex], obtemos respectivamente:
[tex]\qquad \qquad c^2=9+a^2\qquad [/tex] e [tex]\qquad c^2=4+b^2[/tex]
donde segue que:
[tex]\qquad \qquad 4+b^2=9+a^2.\qquad \qquad \textcolor{#800000}{(i)}[/tex]
Mas os muros são paralelos e distantes [tex]5[/tex] metros um do outro; assim, [tex]a+b=5[/tex]. Logo, [tex]a=5-b[/tex] e segue de [tex]\textcolor{#800000}{(i)}[/tex] que:
[tex]\quad 4+b^2=9+(5-b)^2[/tex]
[tex]\quad 4+\cancel{b^2}=9+25-10b+\cancel{b^2}[/tex]
[tex]\quad 10b=34-4[/tex]
[tex]\quad 10b=30[/tex]
[tex]\quad \boxed{b=3 \, m} \, .[/tex]
Como [tex]c^2=4+b^2[/tex], temos que:
[tex]\quad c^2=4+3^2[/tex]
[tex]\quad c^2=13[/tex]
[tex]\quad c=\pm \sqrt{13}[/tex]
[tex]\quad \boxed{c=\sqrt{13}}[/tex], já que [tex]c \gt 0.[/tex]
Assim, o comprimento de cada escada é [tex] \, \fcolorbox{black}{#eee0e5}{$ 3,6 \, metros$} \, [/tex], aproximadamente.
Solução elaborada pelos Moderadores do Blog.
Solução 2
a) Para o comprimento das escadas, adota-se y.
b) As bases dos triângulos são x e 5-x.
c) Utilizando o Teorema de Pitágoras, tem-se que:
I) y²=3²+x²
y²=9+x²
e
II) y²=2²+(5-x)²
d) Substituindo I em II, vem:
y²=2²+(5-x)²
9+x²=4+25-10x+x²
9+x²-4-25+10x-x²=0
10x-20=0
10x=20
x=2.
e) Determinando o valor de y que corresponde ao comprimento da escada
y²=9+x²
y²=9+2²
y²=13
y=√(13)
Logo, o comprimento de cada escada é de aproximadamente 3,6 metros.
Solução elaborada pelo COM OCTETO MATEMÁTICO.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |