Problema
(Indicado a partir do 8º ano do E. F.)
O “Triângulo Russo” trata-se de um problema clássico da Geometria Plana.
Muitos o chamam de “Problema de Langley”, em homenagem ao autor, Edward Mann Langley (1851-1933). Apresentado como exercício em um livro de matemática russo cujo principal autor chamava-se Victor Borisovich Lidskii (1924-2008), esse problema é também conhecido como “Triângulo de Lidskii”.
Vamos a ele.
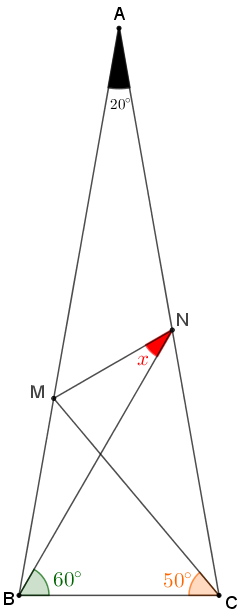
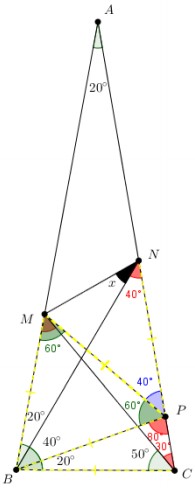
Na figura abaixo, sabendo que os segmentos [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] têm o mesmo comprimento, determine a medida [tex]x[/tex], em graus, do ângulo [tex]B\hat{N}M[/tex].

Lembretes e notação
(1) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
(2) Todo triângulo isósceles possui os lados adjacentes à base congruentes e ângulos da base com mesma medida. (Se precisar, veja o finalzinho desta página.)
(3) Se um triângulo isósceles possui um ângulo interno medindo [tex]60^{\circ}[/tex], então esse triângulo é equilátero.
(4) Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]\overline{AB}[/tex] e o seu comprimento por [tex]AB[/tex].
Solução
Sabemos que a soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ[/tex] (Lembrete (1)). Assim, como [tex]AB = AC[/tex], observando o triângulo [tex]ABC[/tex] concluímos que [tex]A\hat{B}C=A\hat{C}B=80^\circ[/tex]. Podemos, então, construir um segmento de reta com extremidade no ponto [tex]B[/tex] e que intercepta o lado [tex]\overline {AC}[/tex] em um ponto [tex]P[/tex] de tal forma que o ângulo [tex]P\hat{B}C=20^\circ.[/tex]
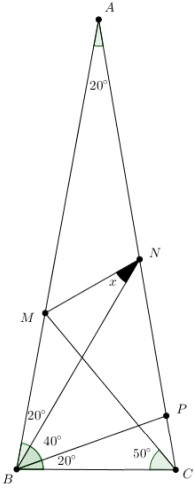
Utilizando o Lembrete (1), vamos explorar a figura anterior e encontrar a medida de vários ângulos.
- Note que no [tex]\triangle PBC[/tex], o ponto [tex]B[/tex] é vértice de um ângulo cuja medida é [tex]20^\circ[/tex] e o ponto [tex]C[/tex] é vértice de um ângulo cuja medida é [tex]80^\circ.[/tex] Logo, concluímos que a medida do ângulo [tex]B\hat{P}C[/tex] é [tex]80^\circ.[/tex]
- Analogamente, no [tex]\triangle BMC[/tex], temos que a medida do ângulo [tex]\hat B[/tex] é [tex] 80^\circ[/tex] e a do ângulo [tex]\hat C [/tex] é [tex] 50^\circ.[/tex] Consequentemente, [tex]\hat M[/tex] mede [tex]50^\circ.[/tex]
- Por fim, no [tex]\triangle PBN[/tex], temos o ângulo que [tex]\hat B[/tex] mede [tex]40^\circ[/tex] e [tex]\hat P[/tex] mede [tex]100^\circ[/tex] (pois a medida de [tex]B\hat{P}C[/tex] é [tex]80^\circ[/tex]). Portanto, [tex]\hat N = 40^\circ.[/tex]
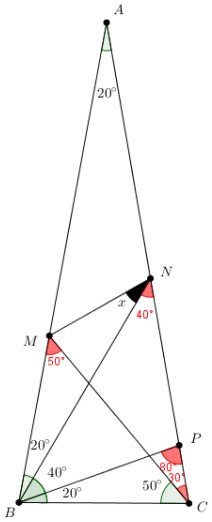
Infelizmente, não conseguimos ainda o valor do ângulo pedido; assim, vamos fazer novas análises,
Na sequência, podemos destacar três triângulos isósceles: [tex]\triangle BPC[/tex], [tex]\triangle PNB[/tex] e [tex]\triangle BMC[/tex]. Observando esses triângulos, concluímos que:
- [tex]BC=BP=PN=BM.[/tex]
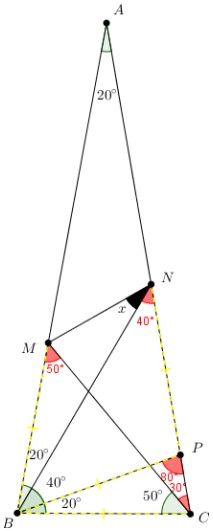
- Agora, perceba que o ângulo [tex]P\hat{B}M[/tex] mede [tex]60^\circ[/tex] e que [tex]BM=BP[/tex]. Portanto, ao construirmos o segmento [tex]\overline{MP}[/tex], percebemos que [tex]\triangle BMP[/tex] é um triângulo equilátero.
- Note também que [tex]PM=PN[/tex]. Logo, o [tex]\triangle PMN[/tex] é isósceles e, portanto, os ângulos da base [tex]P\hat{M}N[/tex] e [tex]P\hat{N}M[/tex] medem [tex]\dfrac{180^\circ-40^\circ}{2}=70^\circ[/tex].
Finalmente, temos que [tex]\boxed{x+40^\circ=70^\circ}[/tex], donde [tex]\fcolorbox{black}{#eee0e5}{$x=30^\circ$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
