 |
Apresentaremos aqui algumas definições e propriedades básicas de semelhança de triângulos para ajudar na resolução dos nossos problemas.
|
Um pouco sobre semelhança de triângulos
O que são triângulos semelhantes?
Vamos relembrar o que são triângulos semelhantes?
Definição:
Dois triângulos são ditos semelhantes quando existe uma correspondência biunívoca entre seus vértices, de modo que
(i) ângulos internos correspondentes são congruentes;
(ii) lados correspondentes são proporcionais.
Na figura abaixo, os triângulos [tex]ABC[/tex] e [tex]DEF[/tex] com a seguinte correspondência entre vértices:
[tex]A\longleftrightarrow D \, \, \, \, \, \, \, \, \, \, [/tex] [tex]B\longleftrightarrow E \, \, \, \, \, \, \, \, \, \, \, \, [/tex] [tex]C\longleftrightarrow F[/tex]
são semelhantes.
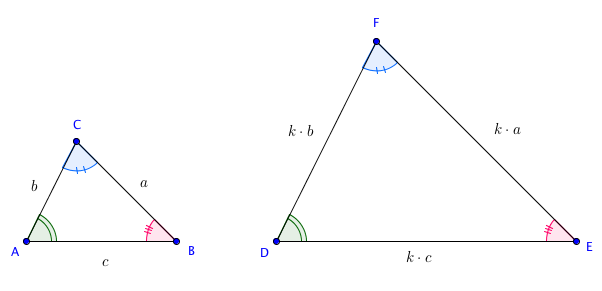
Como os dois triângulos são semelhantes, podemos afirmar que:
● [tex]\widehat{A}[/tex] e [tex]\widehat{D}[/tex] são ângulos congruentes, isto é, ângulos com a mesma medida.
● [tex]\widehat{B}[/tex] e [tex]\widehat{E}[/tex] são ângulos congruentes.
● [tex]\widehat{C}[/tex] e [tex]\widehat{F}[/tex] são ângulos congruentes.
● Os lados correspondentes são proporcionais, isto é, existe um número real positivo [tex]k[/tex], tal que:
[tex] \, \, \, \, \, \, \, \, \, \, \, \, \dfrac{DE}{AB}=\dfrac{EF}{BC}=\dfrac{FD}{CA}=k[/tex].
Observem quantas informações importantes no estudo da geometria vocês conseguem obter sabendo que dois dados triângulos são semelhantes. São três igualdades de medidas de ângulos e três proporcionalidades de comprimentos de segmentos.
Mas o que a definição de semelhança de triângulos nos diz?
► Mas, por outro, é necessário termos em mãos doze medidas para verificarmos se dois dados triângulos são semelhantes:
– as medidas dos três ângulos internos do primeiro triângulo;
– as medidas dos três lados do primeiro triângulo;
– as medidas dos três ângulos internos do segundo triângulo;
– as medidas dos três lados do segundo triângulo.
Assim, para se trabalhar mais confortavelmente com semelhança de triângulos, são necessárias outras informações, além da definição. As próximas propriedades vão ajudar bastante, já que com elas será possível concluir que dois triângulos são semelhantes a partir de um número menor de medidas conhecidas do que as doze que a definição exige. Vejamos.
Casos de semelhança de triângulos
As três propriedades conhecidas como casos (ou critérios) de semelhança são, na verdade, condições mínimas que, se verificadas, nos permitem afirmar que dois triângulos são semelhantes. Será que vocês se lembram delas?
Caso A.A. (ângulo – ângulo):
Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
Caso L.A.L. (lado – ângulo – lado):
Se dois lados de um triângulo são proporcionais a dois lados de outro triângulo e os ângulos internos definidos por esses lados são congruentes, então os triângulos são semelhantes.
Caso L.L.L. (lado – lado – lado):
Se os três lados de um triângulo são proporcionais aos três lados de outro triângulo, então os triângulos são semelhantes.
A próxima propriedade é também um resultado clássico da Geometria Plana e mostrará uma situação muito especial na qual dois triângulos serão sempre semelhantes.
Teorema Fundamental da Proporcionalidade
Teorema:
Se uma reta paralela a um dos lados de um triângulo intersecta os outros dois lados em pontos distintos, então ela determina um triângulo semelhante ao triângulo inicial.
Observem a próxima figura.
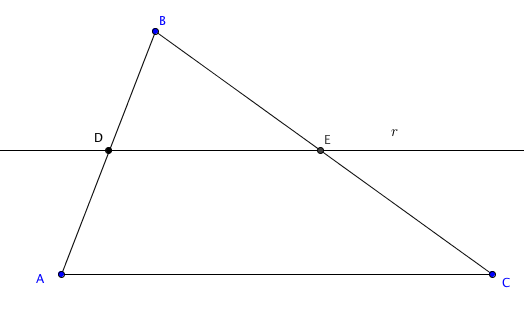
O que o teorema acima nos assegura é que basta sabermos que a reta [tex]r[/tex], determinada pelos pontos [tex]D[/tex] e [tex]E[/tex], é paralela ao lado [tex]AC[/tex] para concluirmos que os triângulos [tex]ABC[/tex] e [tex]DBE[/tex] são semelhantes. Neste caso, a correspondência entre vértices seria:
[tex]A\longleftrightarrow D \, \, \, \, \, \, \, \, \, \, [/tex] [tex]B\longleftrightarrow B \, \, \, \, \, \, \, \, \, \, \, \, [/tex] [tex]C\longleftrightarrow E[/tex]
As demonstrações dos quatro resultados enunciados não serão discutidas nesta sala, pois fogem do nosso objetivo neste momento, que é apenas relembrarmos fatos importantes da semelhança de triângulos.
Equipe COM – OBMEP
Julho de 2018.
