Problema
(Indicado a partir do 2º ano do E. M.)
O gráfico de barras abaixo exibe a distribuição das idades dos jovens presentes em um Encontro Olímpico de Matemática.
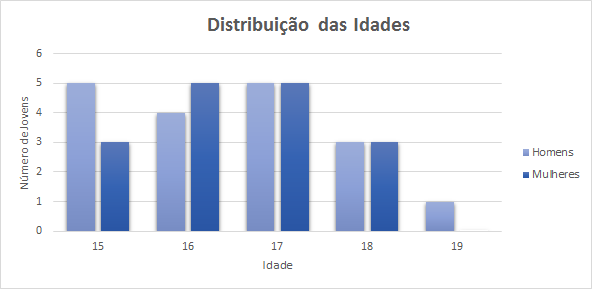
a) Mostre que, nesse grupo, a idade média dos homens é igual à idade média das mulheres.
b) Escolhendo ao acaso um homem e uma mulher desse grupo, determine a probabilidade de que a soma das idades seja menor que [tex]36[/tex] anos.
Solução
a) Seja [tex]M_H[/tex] a média das idades dos homens e [tex]M_M[/tex] a média das idades das mulheres. Dessa forma,
[tex]\qquad \boxed {M_H=\dfrac{5\times 15+4\times 16+5\times 17+3\times 18+19}{5+4+5+3+1}=\dfrac{297}{18}=16,5 \, anos}[/tex]
e
[tex]\qquad \boxed {M_M=\dfrac{3\times 15+5\times 16+5\times 17+3\times 18}{3+5+5+3}=\dfrac{264}{16}=16,5 \, anos}.[/tex]
b) De modo a reduzir as contas, utilizaremos a ideia de probabilidade complementar para responder a este item: calcularemos a probabilidade de a soma das idades ser maior do que ou igual a [tex]36[/tex] anos (são poucos casos) e aplicaremos o cálculo de probabilidade complementar.
Para tal, veja que ao considerarmos que a soma das idades é maior do que ou igual a [tex]36[/tex] anos, temos apenas duas situações: a soma pode ser [tex]36[/tex] ou [tex]37[/tex], já os dados apresentados permitem apenas essas duas somas. Assim, vamos considerar essas situações:
- a soma é [tex]36[/tex]: um homem e uma mulher de [tex]18[/tex] anos ou um homem de [tex]19[/tex] anos e uma mulher de [tex]17[/tex] anos;
- a soma é [tex]37[/tex]: uma mulher de [tex]18 \, [/tex] e um homem de [tex]19[/tex] anos.
Vamos, então, considerar cada um dos eventos disjuntos a seguir, para contar os casos favoráveis para obter soma maior do que ou igual a [tex]36[/tex]:
- i) Escolher um homem e uma mulher de [tex]18[/tex] anos:
Note que existem [tex]3[/tex] homens e [tex]3[/tex] mulheres com [tex]18[/tex] anos, assim podem ser formadas [tex]\boxed{3\times 3=9}[/tex] duplas cuja soma das idades seja [tex]36[/tex].
ii) Escolher um homem de [tex]19[/tex] anos e uma mulher de [tex]17[/tex] anos:
De modo análogo ao caso anterior, podem ser formadas [tex]\boxed{1\times 5=5}[/tex] duplas, pois a quantidade de homens com [tex]19[/tex] anos é [tex]1[/tex] e a de mulheres com [tex]17[/tex] anos é [tex]5[/tex].
iii) Escolher um homem de [tex]19[/tex] anos e uma mulher de [tex]18[/tex] anos:
Neste caso, podem ser formadas [tex]\boxed{1\times 3=3}[/tex] duplas, pois a quantidade de homens com [tex]19[/tex] anos é [tex]1[/tex] e a de mulheres com [tex]18[/tex] anos é [tex]3 \, .[/tex]
Assim, são [tex]\boxed{9+5+3=17}[/tex] casos favoráveis à soma das idades ser igual a ou maior do que [tex]36[/tex] e existem [tex]\boxed{18\times 16}[/tex] duplas no total.
Dessa forma, a probabilidade de a soma ser maior do que ou igual a [tex]36[/tex] é dada por [tex] \, \fcolorbox{#800000}{#ffffff}{$\textcolor{#800000}{P_{S\geqslant 36}=\dfrac{17}{18\times 16}}$} \, .[/tex]
Para concluirmos a questão, basta observar que a probabilidade de que a soma das idades seja menor que [tex]36[/tex] anos pode ser assim calculada:
[tex]\qquad \fcolorbox{black}{#eee0e5}{$P_{S\lt36}=1-P_{S\geq 36}=1-\dfrac{17}{18\times 16}=\dfrac{271}{288}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
