Nesta sala, veremos mais um método prático e direto para resolver sistemas lineares com o mesmo número de equações e incógnitas.
Teorema de Cramer
Consideremos um sistema linear em que o número de equações é igual ao número de incógnitas. Nessas condições, [tex]A[/tex] (matriz incompleta do sistema) é uma matriz quadrada. A partir de agora, consideraremos [tex]D=\det A.[/tex]
onde [tex]D_{\alpha_i}[/tex] é o determinante da matriz obtida a partir de [tex]A[/tex], substituindo-se a [tex]i[/tex]-ésima coluna pela coluna dos termos independentes das equações do sistema.
Agora que já compreendemos o Teorema de Cramer, vamos colocar o que aprendemos em prática.
➤ Exemplo 1: Vamos resolver o sistema [tex]\begin{cases}
x&+&y&+&z&=&6 \\
2x&+&3y&-&z&=&5 \\
x&-&y&-&z&=&-4
\end{cases}.[/tex]
Inicialmente, vamos calcular o determinante da matriz [tex]A[/tex] associada ao sistema:
1 & 1 & 1 \\
2 & 3 & -1 \\
1 & -1 & -1
\end{bmatrix}.[/tex]
Temos
1 & 1 & 1 \\
2 & 3 & -1 \\
1 & -1 & -1
\end{vmatrix}
=-3-1-2-3-1+2=-8.[/tex]
Agora, vamos determinar [tex]D_x, D_y[/tex] e [tex]D_z,[/tex] ou seja, os determinantes das matrizes obtidas pela substituição dos termos que são coeficientes de [tex]x, y[/tex] e [tex]z[/tex], respectivamente, pelos termos independentes:
- [tex]D_x=\begin{vmatrix}
6 & 1 & 1 \\
5 & 3 & -1 \\
-4 & -1 & -1
\end{vmatrix}
=-18+4-5+12-6+5=-8;[/tex] - [tex]D_y=\begin{vmatrix}
1 & 6 & 1 \\
2 & 5 & -1 \\
1 & -4 & -1
\end{vmatrix}
=-5-6-8-5-4+12=-16;[/tex] - [tex]D_z=\begin{vmatrix}
1 & 1 & 6 \\
2 & 3 & 5 \\
1 & -1 & -4
\end{vmatrix}
=-12+5-12-18+5+8=-24.[/tex]
Finalmente, temos:
Assim, o sistema resolvido possui solução única [tex](1, 2, 3)[/tex]. Nesse sentido, podemos classificá-lo como Sistema Possível (ou Compatível) e Determinado.
Portanto, escrevemos a solução desse sistema como sendo [tex]\mathcal{S} = \{(1, 2, 3)\}.[/tex]
|
No exemplo acima obtivemos [tex]D\neq 0,[/tex] mas o que aconteceria se, em vez disso, tívessemos [tex]D=0[/tex]? |
 |
 |
Essa é uma excelente pergunta. Embora não consigamos utilizar o teorema de Cramer em casos como esse, podemos tirar conclusões acerca das soluções desse sistema, se é que ele vai ter solução… |
Para responder a essa pergunta, vamos analisar, por exemplo, o sistema
ax&+&by&=&c \\
dx&+&ey&=&f
\end{cases},[/tex]
Inicialmente, vamos escalonar o sistema. Para isso, vamos multiplicar a segunda equação por [tex]a,[/tex] obtendo assim o sistema equivalente
ax&+&by&=&c \\
adx&+&aey&=&af
\end{cases}.[/tex]
Agora, multipliquemos a primeira equação por [tex](-d)[/tex] e somemos à segunda equação, obtendo
ax&+&by&=&c \\
aey&-&bdy&=&af-cd
\end{cases}\Longrightarrow \begin{cases}
ax+by&=&c \\
(ae-bd)y&=&af-cd
\end{cases}.[/tex]
Como estamos admitindo [tex]D = 0[/tex] (e portanto [tex]ae-bd=0[/tex]), se na segunda equação tivermos [tex]af-cd\neq 0[/tex] o sistema será impossível, ou seja, se [tex]D_y\neq 0[/tex] o sistema não admite solução.
Se, por outro lado, multiplicássemos a segunda equação do sistema inicial por [tex]b,[/tex] teríamos o sistema equivalente
ax&+&by&=&c \\
bdx&+&bey&=&bf
\end{cases}.[/tex]
Agora, multiplicando a primeira equação por [tex](-e)[/tex] e somando à segunda equação, obtemos
ax&+&by&=&c \\
bdx&-&aex&=&bf-ce
\end{cases}\Longrightarrow \begin{cases}
ax+by&=&c \\
(bd-ae)x&=&bf-ce
\end{cases}.[/tex]
Novamente, como estamos admitindo [tex]D = 0[/tex] (e portanto [tex]bd-ae=0[/tex]), se na segunda equação tivermos [tex]bf-ce\neq 0[/tex] o sistema será impossível, ou seja, se [tex]D_x\neq 0[/tex] o sistema não admite solução.
Isso que acabamos de ver se aplica a qualquer sistema que possui o número de equações igual ao número de incógnitas. Assim, podemos generalizar esse resultado:
- se [tex]D_{\alpha_i}\neq 0,[/tex] para algum [tex]i\in \{1, 2, 3, \dots, n\},[/tex] então o sistema é impossível;
- se [tex]D_{\alpha_i}=0, \forall i\in \{1, 2, 3, \dots, n\},[/tex] então o sistema é possível e indeterminado;
➤ Exemplo 2: Vamos resolver o sistema [tex]\begin{cases}
x&+&y&+&z&=&0 \\
x&-&y&+&z&=&2 \\
x&+&2y&+&z&=&-1
\end{cases}.[/tex]
Inicialmente, vamos calcular o determinante da matriz [tex]A[/tex] associada ao sistema:
1 & 1 & 1 \\
1 & -1 & 1 \\
1 & 2 & 1
\end{bmatrix}.[/tex]
Temos
1 & 1 & 1 \\
1 & -1 & 1 \\
1 & 2 & 1
\end{vmatrix}
=-1+1+2+1-2-1=0.[/tex]
Como obtivemos [tex]D=0[/tex], pelo teorema de Cramer, o sistema não se classifica como possível e determinado. Resta analisar se o sistema é Possível e Indeterminado ou Impossível. Para isso, vamos determinar [tex]D_x, D_y[/tex] e [tex]D_z:[/tex]
- [tex]D_x=\begin{vmatrix}
0 & 1 & 1 \\
2 & -1 & 1 \\
-1 & 2 & 1
\end{vmatrix}=0-1+4-1-0-2=0.[/tex] - [tex]D_y=\begin{vmatrix}
1 & 0 & 1 \\
1 & 2 & 1 \\
1 & -1 & 1
\end{vmatrix}=2-0-1-2+1-0=0.[/tex] - [tex]D_z=\begin{vmatrix}
1 & 1 & 0 \\
1 & -1 & 2 \\
1 & 2 & -1
\end{vmatrix}=1+2+0+0-4+1=0.[/tex]
Como encontramos [tex]D_x=D_y=D_z=0,[/tex] neste caso o sistema é classificado como Sistema Possível e Indeterminado, ou seja, o sistema possui infinitas soluções.
|
E como achar essas infinitas soluções? |
 |
Sem perda de generalidade, tomamos [tex]z[/tex] como a variável livre — isto é, aquela que pode assumir qualquer valor real — e determinamos as demais variáveis em função dessa escolha. Porém, utilizaremos apenas duas das três equações. Dessa forma, nosso sistema se torna o seguinte:
x&+&y&=&-z \\
x&-&y&=&2-z
\end{cases}.[/tex]
Agora, adicionando as duas equações, obtemos:
e substituindo esse valor de [tex]x[/tex] na primeira equação, obtemos o valor correspondente de [tex]y[/tex]:
Finalmente, a solução do sistema é dada pelo terno ordenado [tex](x, y, z)=(1-z, -1, z)[/tex], onde [tex]z\in \mathbb{R}[/tex] é a variável livre.
Para cada valor real de [tex]z[/tex], temos um terno que é solução do sistema, por isso há infinitas soluções nesse tipo de sistema. Por exemplo,
- para [tex]z=0,[/tex] encontramos a solução [tex](1, -1, 0)[/tex];
- para [tex]z=1,[/tex] encontramos a solução [tex](0, -1, 1)[/tex];
- para [tex]z=-1,[/tex] encontramos a solução [tex](2, -1, -1)[/tex], e assim sucessivamente.
Portanto, escrevemos o conjunto solução desse sistema como sendo [tex]\mathcal{S}=\{(1-z, -1, z); z\in \mathbb{R}\}.[/tex]
➤ Exemplo 3: Vamos resolver o sistema [tex]\begin{cases}
x&+&y&+&z&=&2 \\
2x&+&3y&+&z&=&5 \\
3x&+&4y&+&2z&=&8
\end{cases}.[/tex]
Inicialmente, vamos calcular o determinante da matriz [tex]A[/tex] associada ao sistema:
1 & 1 & 1 \\
2 & 3 & 1 \\
3 & 4 & 2
\end{bmatrix}.[/tex]
Logo,
1 & 1 & 1 \\
2 & 3 & 1 \\
3 & 4 & 2
\end{vmatrix}
=6+3+8-9-4-4=0.[/tex]
Como obtivemos [tex]D=0[/tex], pelo teorema de Cramer, o sistema não se classifica como possível e determinado. Resta analisar se o sistema é Possível e Indeterminado ou Impossível. Para isso, vamos determinar [tex]D_x[/tex]:
2 & 1 & 1 \\
5 & 3 & 1 \\
8 & 4 & 2
\end{vmatrix}=12+8+20-24-8-10=-2.[/tex]
Como encontramos [tex]D_x\neq 0,[/tex] já podemos parar por aqui, pois neste caso o sistema é classificado como Sistema Impossível (ou Incompatível), ou seja, o conjunto solução é [tex]\mathcal{S} = \emptyset[/tex].
Interpretação Geométrica de Sistemas Lineares com Duas Variáveis
Consideremos um sistema linear com duas equações e duas incógnitas:
\begin{cases}
ax&+&by&=&c \\
dx&+&ey&=&f
\end{cases},[/tex]
onde [tex]a, b, c, d, e, f[/tex] são constantes reais e [tex]x, y[/tex] são as duas incógnitas.
A interpretação geométrica desse sistema está associada à representação das equações como retas no plano cartesiano.
Casos Possíveis
Exemplo: Observe o sistema [tex]
\begin{cases}
x&+&y&=&4 \\
x&-&y&=&0
\end{cases}.[/tex]
As retas das equações do sistema estão representadas abaixo.
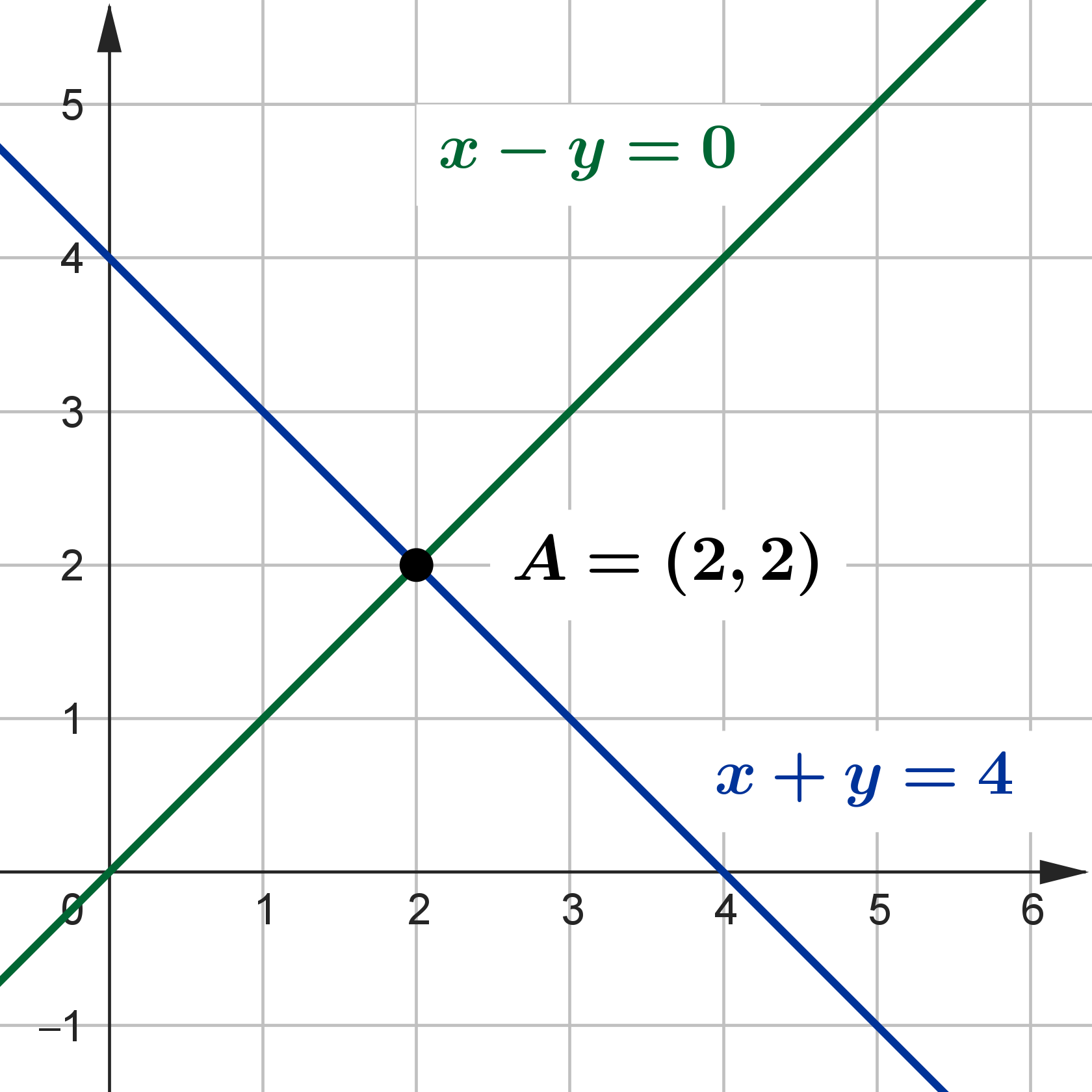
Perceba que a única intersecção das retas ocorre no ponto [tex]A=(2, 2)[/tex], ou seja, o sistema admite uma única solução e, portanto, é Possível (ou Compatível) e Determinado. Sua solução é [tex]\mathcal{S}=\{(2, 2)\}[/tex].
➤ Sistema Possível e Indeterminado (SPI): Se as duas equações representam a mesma reta, ou seja, uma equação é múltipla da outra, então o sistema possui infinitas soluções, correspondendo a todos os pontos dessa reta.
Exemplo: Observe o sistema [tex]
\begin{cases}
x&+&y&=&4 \\
2x&+&2y&=&8
\end{cases}.[/tex]
As retas das equações do sistema estão representadas abaixo.
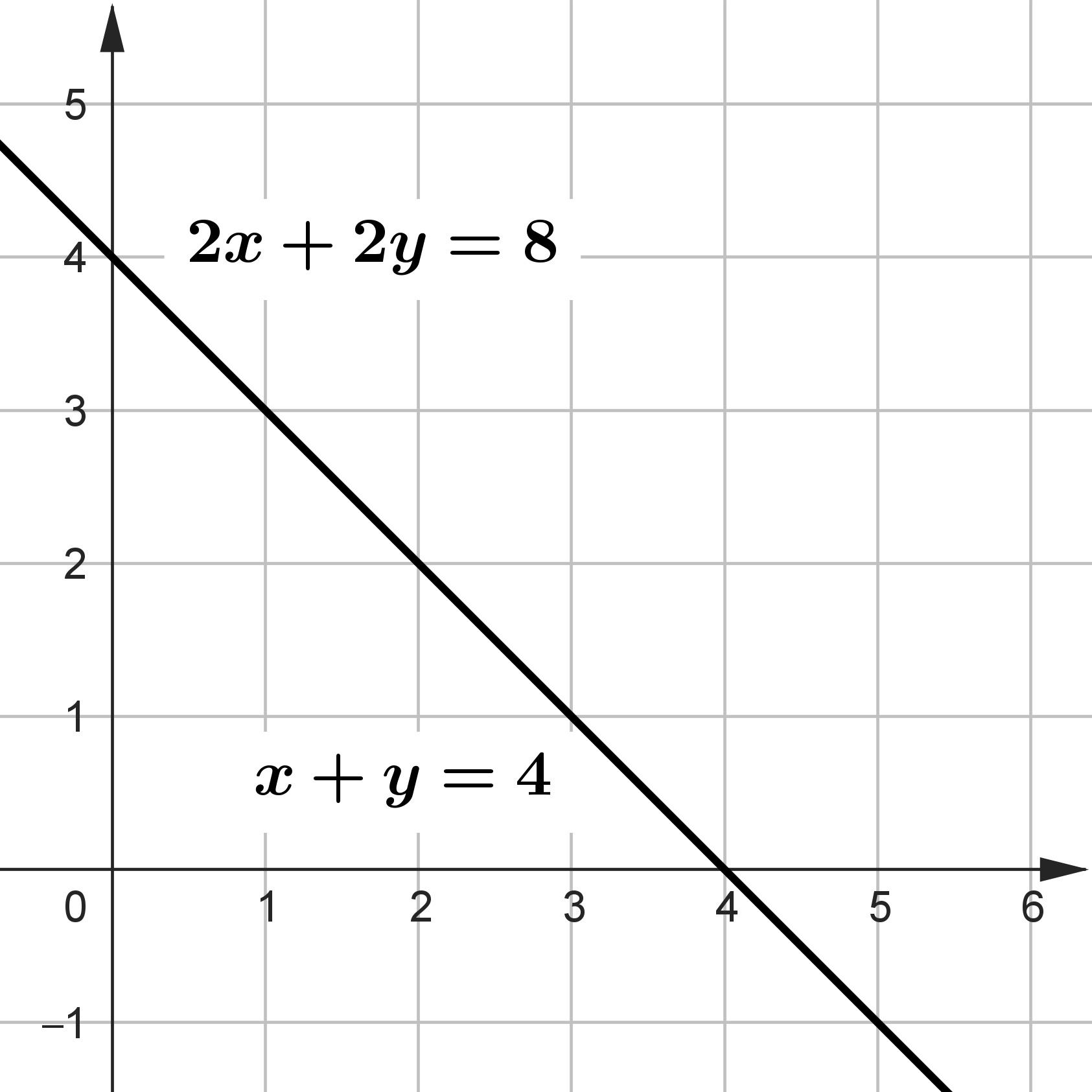
Perceba que as duas retas coincidem, ou seja, o sistema admite uma infinidade de soluções, e, portanto, é Possível (ou Compatível) e Indeterminado, e sua solução é [tex]\mathcal{S}=\{(4-y, y); y\in \mathbb{R}\}[/tex].
➤ Sistema Impossível (SI): Se as equações representam retas paralelas distintas, então não existe solução, pois as retas nunca se interceptam.
Exemplo: Observe o sistema [tex]
\begin{cases}
x&+&y&=&4 \\
x&+&y&=&5
\end{cases}.[/tex]
As retas das equações do sistema estão representadas abaixo.
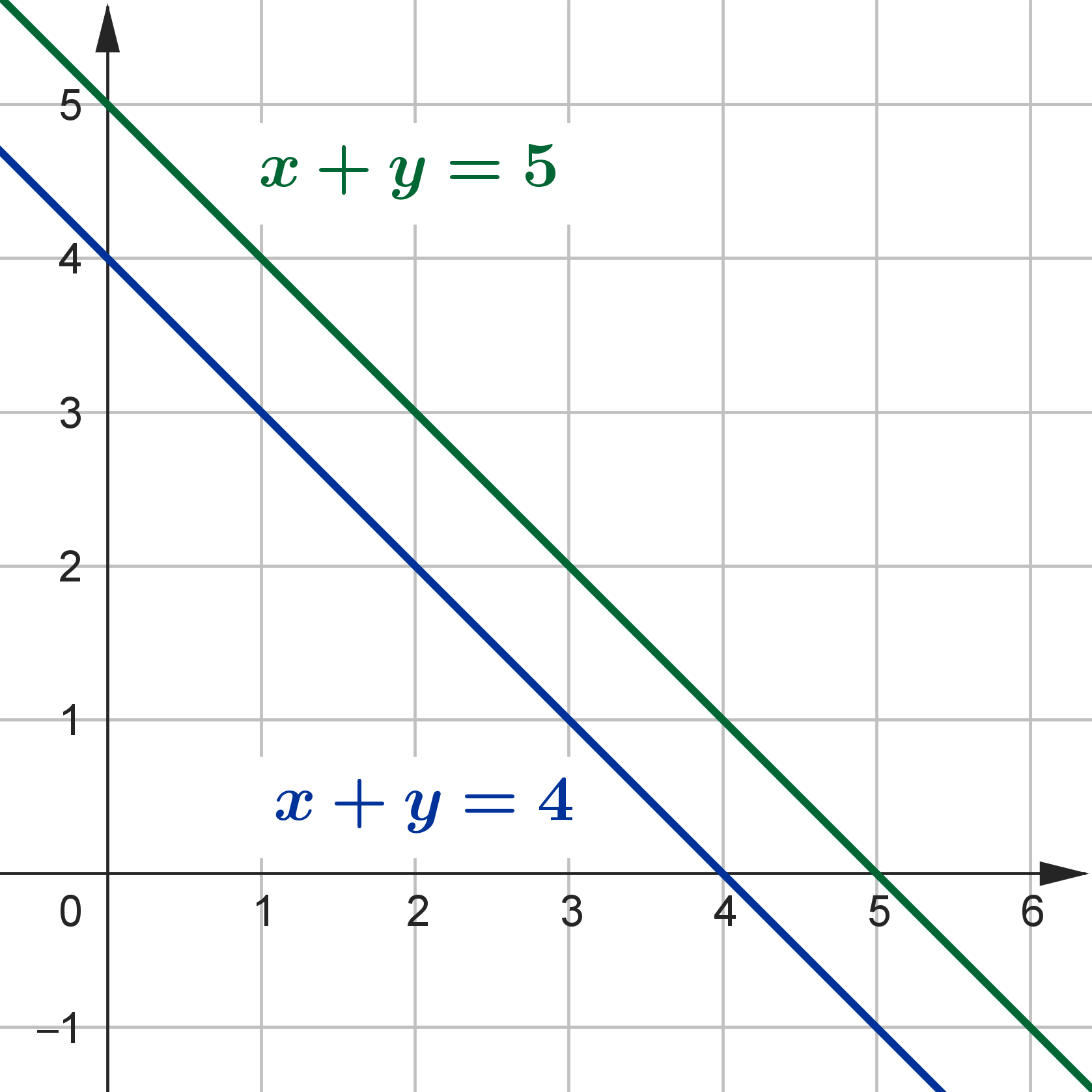
Perceba que as duas retas não se intersectam, ou seja, o sistema não admite nenhuma solução, e, portanto, é Impossível (ou Incompatível), e sua solução é [tex]\mathcal{S}=\emptyset[/tex].
Determinação das Condições
Dado o sistema linear com duas incógnitas
\begin{cases}
ax&+&by&=&c \\
dx&+&ey&=&f
\end{cases},[/tex]
onde [tex]a, b, c, d, e, f[/tex] são constantes reais e [tex]x, y[/tex] são as variáveis desconhecidas, sua classificação quanto ao número de soluções pode ser feita a partir dos coeficientes das equações:
➤ Se [tex]\dfrac{a}{d}\neq \dfrac{b}{e}[/tex], as retas são concorrentes e o sistema é SPD;
➤ Se [tex]\dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f}[/tex], as equações são da mesma reta e o sistema é SPI;
➤ Se [tex]\dfrac{a}{d}=\dfrac{b}{e}\neq \dfrac{c}{f}[/tex], as retas são paralelas e distintas, tornando o sistema SI.
A interpretação geométrica de um sistema linear com duas incógnitas é uma ferramenta fundamental para compreender sua solução. Ao visualizar as equações como retas no plano, podemos identificar rapidamente a existência e a quantidade de soluções, facilitando a análise e resolução do sistema.
Equipe COM – OBMEP
