Definição: Chamamos de progressão aritmética (P.A.) toda sequência numérica em que cada termo, a partir do segundo, é igual à soma do termo anterior com uma constante. Essa constante é chamada razão da P.A. e é usualmente indicada por [tex]r[/tex].
Observação: Progressões aritméticas podem ser finitas ou infinitas.
Exemplos:
● Quando [tex]a_1=1[/tex] e [tex]r=2,[/tex] temos a P.A. [tex](1,3,5,7,\cdots).[/tex]
● Quando [tex]a_1=2[/tex] e [tex]r=1,5,[/tex] temos a P.A. [tex](2;~3,5;~5;~6,5;\cdots).[/tex]
● Quando [tex]a_1=-3[/tex] e [tex]r=0,[/tex] temos a P.A. [tex](-3, -3, -3, \cdots).[/tex]
● Quando [tex]a_1=0[/tex] e [tex]r=-3,[/tex] temos a P.A. [tex](0,-3,-6,-9,\cdots).[/tex]
Classificação
As progressões aritméticas podem ser classificadas em três categorias, conforme veremos a seguir.
De fato,
[tex]\qquad \quad a_2 = a_1+r = a_1+0=a_1[/tex];
[tex]\qquad\quad a_3 = a_2+r=a_1+0=a_1[/tex];
[tex]\qquad\quad a_4=a_3+r =a_1+0=a_1[/tex];
[tex]\qquad ~~~~~~\vdots [/tex]
Exemplo: [tex](3,3,3,\cdots)[/tex] é uma progressão aritmética constante, na qual [tex]a_1=3[/tex] e [tex]r=0.[/tex]
➤ Crescentes: são progressões aritméticas cuja razão é positiva ([tex]r\gt 0[/tex]). Neste caso, cada termo, a partir do segundo, é maior que o termo anterior.
Vejamos: se [tex]r\gt 0[/tex], segue que:
[tex]\qquad\quad a_2 = a_1+r\gt a_1[/tex];
[tex]\qquad\quad a_3 = a_2+r\gt a_2[/tex];
[tex]\qquad\quad a_4 = a_3+r\gt a_3[/tex];
[tex]\qquad\quad a_5 = a_4+r\gt a_4[/tex];
[tex]\qquad ~~~~~~\vdots[/tex]
Exemplo: [tex](0,2,4,6,8\cdots)[/tex] é uma progressão aritmética crescente, na qual [tex]a_1=0[/tex] e [tex]r=2.[/tex]
➤ Decrescentes: são progressões aritméticas cuja razão é negativa ([tex]r\lt 0[/tex]). Neste caso, cada termo, a partir do segundo, é menor que o termo anterior.
Observe: se [tex]r\lt 0[/tex], segue que:
[tex]\qquad \quad a_2 = a_1+r\lt a_1[/tex];
[tex]\qquad\quad a_3 = a_2+r\lt a_2[/tex];
[tex]\qquad\quad a_4 = a_3+r\lt a_3[/tex];
[tex]\qquad\quad a_5 = a_4+r\lt a_4[/tex];
[tex]\qquad ~~~~~~\vdots[/tex]
Exemplo: [tex](0,-3,-6,-9,\cdots)[/tex] é uma progressão aritmética decrescente, na qual [tex]a_1=0[/tex] e [tex]r=-3.[/tex]
Termo geral de uma P.A.
Nesta seção, veremos que um termo qualquer de uma P.A. (finita ou infinita) pode ser imediatamente determinado, conhecendo-se apenas o primeiro termo [tex]a_1[/tex] e a razão [tex]r[/tex] da P.A. em questão.
Veja que, se considerarmos os temos [tex]a_1,~a_2,~\cdots~,~a_n[/tex] de qualquer progressão aritmética de razão [tex]r[/tex], por definição teremos:
[tex]\qquad \begin{align}a_2 &= a_1+r;\\
a_3&= a_2+r = (a_1+r)+r = a_1+2r;\\
a_4&=a_3+r=(a_1+2r)+r=a_1+3r;\\
&~~ \vdots\\
a_n&=a_{n-1}+r=(a_1+(n-2)\cdot r)+r=a_1+(n-1)\cdot r;\\
~~\end{align} [/tex]
Assim, pelo que acabamos de deduzir, existe uma fórmula para encontrar o n-ésimo termo de uma P.A.; vamos registrar essa fórmula como uma propriedade.
[tex]\qquad \boxed{a_n=a_1+(n-1)\cdot r}[/tex]
com [tex]n \in \mathbb{N}^*.[/tex]
A fórmula anterior é bastante útil, porém tem a inconveniência de precisarmos do primeiro termo da progressão e isso nem sempre é possível. Veremos a seguir outra maneira de obtermos termos de uma progressão aritmética: a partir de qualquer termo anterior da progressão. Mas, para isso, a fórmula anterior é o primeiro passo da dedução:
[tex]\qquad a_n = a_1+(n-1)\cdot r[/tex]
[tex]\qquad a_n = a_1+(p+n-1-p)\cdot r[/tex]
[tex]\qquad a_n = a_1+[(p-1)+(n-p)]\cdot r[/tex]
[tex]\qquad a_n = \underbrace{a_1+(p-1)\cdot r}_{a_p}+ (n-p)\cdot r[/tex]
[tex]\qquad a_n = a_p+ (n-p)\cdot r.[/tex]
Também vamos registrar essa fórmula como uma propriedade.
[tex]\boxed{a_n = a_p+ (n-p)\cdot r}[/tex]
com [tex]n,~p \in \mathbb{N}^*[/tex] tais que [tex] p \lt n.[/tex]
Soma dos [tex]n[/tex] primeiros termos de uma P.A.
 Imagem extraída da Revista Galileu
Imagem extraída da Revista Galileu
O cálculo feito pelo menino foi:
[tex] \boxed{1+2+3+\cdots +99+100=\dfrac{100}{2} \times 101 = 50\times 101=5050}.[/tex]
Entenda a peripécia do garoto, observando o esqueminha abaixo.
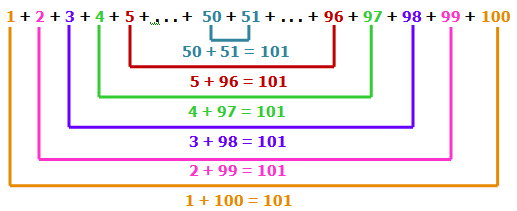
Para a história não ficar sem fim, o menino autor da façanha se tornou um dos mais importantes matemáticos de todos os tempos: Johann Carl Friedrich Gauss, conhecido como o Príncipe da Matemática!
Note que a sequência [tex](1,2,3,\cdots, 100)[/tex] é uma P.A. de razão [tex]1.[/tex] Assim, como Gauss, vamos tentar obter a soma dos termos iniciais [tex]a_1,~a_2,~a_3,~\cdots~,~a_n[/tex] de uma P.A.; só que de uma P.A. qualquer:
[tex]\qquad \begin{align}S_n &= a_1+a_2+\cdots +a_n\\
&= a_1+(a_1+r)+\cdots +(a_1+(n-1)\cdot r).\end{align}[/tex]
Uma outra maneira de escrevermos [tex]S_n[/tex], seria
[tex]\qquad \begin{align}S_n &= a_n+a_{n-1}+\cdots +a_1\\
&= a_n+(a_n-r)+\cdots +(a_n-(n-1)\cdot r).\end{align}[/tex]
Somando as expressões encontradas na primeira e na segunda maneiras de representar [tex]S_n[/tex], temos:
[tex]\begin{align}&S_n = a_1+(a_1~\cancel{+r})+\cdots +(a_1~\cancel{+(n-1)\cdot r})\\
+~~& \\
&S_n = a_n+(a_n~\cancel{-r})+\cdots +(a_n~\cancel{-(n-1)\cdot r})\end{align}\\
\\
\underline{~\qquad \qquad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}[/tex]
[tex] ~~~~ 2S_n = \underbrace{(a_1+a_n)+(a_1+a_n)+\cdots +(a_1+a_n)}_{\mbox{n vezes}}[/tex]
[tex] ~~~~ 2S_n = (a_1+a_n)\cdot n[/tex]
[tex] ~~~~~ \boxed{S_n = \dfrac{(a_1+a_n)\cdot n}{2}}[/tex].
Vamos registrar mais essa propriedade e aplicá-la em dois exercícios.
Denotando por [tex]S_n[/tex] a soma dos [tex]n[/tex] primeiros termos dessa P.A., temos
[tex]\qquad \boxed{S_n = \dfrac{(a_1+a_n)\cdot n}{2}}. [/tex]
Dois exercícios resolvidos:
(1) Determine a soma de todos os números pares de três algarismos.
- Solução: O menor número par de três algarismos é [tex]100[/tex] e o maior é [tex]998[/tex]; queremos, então, saber a soma dos termos da sequência [tex](100, 102, 104, \cdots, 998)[/tex].
Para isso, precisamos saber quantos termos tem essa sequência.
Observe que o primeiro termo é [tex]a_1=100[/tex] e a razão é [tex]r=2[/tex].
Fazendo [tex]a_n=998[/tex], vamos determinar o valor de [tex]n[/tex].
Pela fórmula do termo geral da P.A., temos:
[tex]\qquad a_n = a_1+(n-1)\cdot r\\
\qquad 998 = 100+(n-1)\cdot 2\\
\qquad 898=(n-1)\cdot 2\\
\qquad n-1=449\\
\qquad n=450.[/tex]
Portanto, usando agora a fórmula da soma dos termos da P.A., segue que:
[tex]\qquad S_{450} = \dfrac{(100+998)\cdot 450}{2}\\
\qquad S_{450} = \dfrac{1\;098\cdot 450}{2}\\
\qquad \boxed{S_{450} = 247\;050}.[/tex]
(2) Determine a soma dos 15 primeiros termos da P.A. [tex](-4,-1,2,5,\cdots).[/tex]
- Solução: Note que nessa progressão temos [tex]a_1= -4[/tex] e [tex]r=3.[/tex]
A princípio, não podemos aplicar a fórmula da Soma dos termos de uma P.A., pois não conhecemos o décimo quinto termo. Mas podemos obtê-lo com a “Fórmula do termo geral de uma P.A.”:
[tex]\qquad a_{15}=a_1+(15-1)\cdot r\\
\qquad a_{15}=-4+(15-1)\cdot 3\\
\qquad a_{15}=-4+42=38.[/tex]
Agora, pela “Fórmula da soma dos termos de uma P.A.”, segue que:
[tex]\qquad S_{15} = \dfrac{(a_1+a_{15})\cdot 15}{2}\\
\qquad S_{15} = \dfrac{(-4+38)\cdot 15}{2}\\
\qquad S_{15} = \dfrac{34\cdot 15}{2}\\
\qquad S_{15}=255.[/tex]
Para utilizarmos o resultado obtido para se calcular “a soma dos primeiros termos de uma P.A.”, precisamos conhecer o “primeiro termo”, o “termo que define a última parcela da soma” e a “quantidade total de termos a serem somados”. Mas o exercício anterior nos mostra que podemos obter essa soma conhecendo o valor [tex]a_1[/tex] do primeiro termo, a razão [tex]r[/tex] e a quantidade [tex]n[/tex] de termos a serem somados.
Então, genericamente, vamos considerar uma P.A. cujos termos são [tex]a_1,~a_2,a_3,~\cdots~~[/tex], a razão seja [tex]r[/tex] e tentar obter a soma [tex]S_n[/tex] dos [tex]n[/tex] primeiros termos dessa P.A..
Usando o resultado visto anteriormente, temos [tex]S_n = \dfrac{(a_1+a_n)n}{2}[/tex]; mas, substituindo nessa fórmula o termo geral [tex]\textcolor{#42c1a6}{\boxed{a_n= a_1+(n-1)\cdot r}}[/tex], segue que:
[tex]\qquad S_n = \dfrac{(a_1+\textcolor{#42c1a6}{a_n})n}{2}\\
\qquad S_n = \dfrac{\left[a_1+\textcolor{#42c1a6}{\boxed{a_1+(n-1)\cdot r}}\right]n}{2}\\
\qquad S_n = \dfrac{\left[2a_1+(n-1)\cdot r\right]n}{2}\\
\qquad S_n = \dfrac{2na_1+n(n-1)\cdot r}{2}\\
\qquad S_n = na_1+\dfrac{n(n-1)}{2}\cdot r.[/tex]
Dessa forma, temos uma alternativa para calcular a soma dos primeiros termos de uma P.A.:
Denotando por [tex]S_n[/tex] a soma dos [tex]n[/tex] primeiros termos dessa P.A., temos que
[tex]\qquad \boxed{S_n = n\cdot a_1+\dfrac{n\cdot (n-1)}{2}\cdot r}. [/tex]
A geometria das Progressões Aritméticas
Uma progressão aritmética pode ser interpretada geometricamente como uma sequência de pontos sobre uma reta, a uma igual distância dos seus dois vizinhos imediatos, conforme ilustra a próxima imagem.
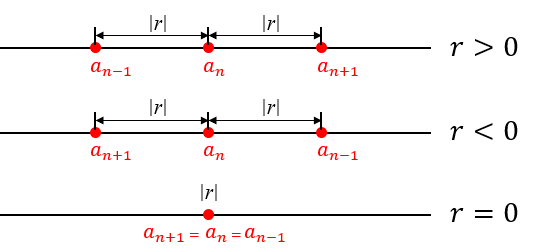
Formalizando, temos mais uma propriedade, a quarta e última que será apresentada nesta Sala e que garante, que olhando os termos de uma PA como pontos de uma reta, cada termo a partir do segundo é o ponto médio de seus vizinhos imediatos:
[tex]\boxed{a_n = \dfrac{a_{n-1}+a_{n+1}}{2}}[/tex]
para [tex]n \in \mathbb{N},~ n \gt 1.[/tex]
Podemos garantir esse resultado de maneira bem simples.
De fato, observe que:
[tex]\quad \qquad \begin{align} \boxed{\dfrac{a_{n-1}+a_{n+1}}{2}} &= \dfrac{a_{n-1}+(a_{n-1}+2r)}{2}\\
&=\dfrac{2a_{n-1}+2r}{2}\\
&=a_{n-1}+r\\
&=\boxed{a_n}.\end{align}[/tex]
Finalizando, aí vai o último exercício desta Sala.
Exercício: Sabendo que a sequência [tex](3x-5, 3x+1, 25)[/tex] é uma P.A., determine o valor de [tex]x[/tex].
- Solução: Usando a propriedade vista acima, temos o seguinte:
[tex]\qquad a_2 = \dfrac{a_1+a_3}{2}\\
\qquad 3x+1 = \dfrac{3x-5+25}{2}\\
\qquad 3x+1 = \dfrac{3x+20}{2}\\
\qquad 6x+2=3x+20\\
\qquad 3x=18\\
\qquad \boxed{x=6}.[/tex]
Equipe COM – OBMEP
