Problema
(Indicado a partir do 9º ano do E. F.)
Uma empresa usa, para um determinado produto, as embalagens fechadas da figura, confeccionadas com o mesmo material, cujo [tex]\text{ cm}^2[/tex] custa [tex]R\$\,0,10[/tex].
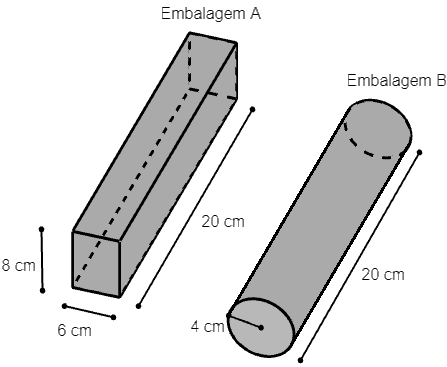
Qual embalagem é mais econômica e qual é a diferença de custo entre os dois modelos? Utilize [tex]\pi\approx 3,14[/tex].
Adaptado de Conquistando a Matemática no ENEM – 2015.
Solução
A embalagem A é um paralelepípedo. Observe que sua área superficial é a soma das áreas de seis retângulos, dois a dois congruentes (as faces opostas são iguais). Esta área é dada por
[tex]\qquad A=2\times(8\times 6+8\times 20+6\times 20)=2\times(48+160+120)=2\times 328=656\text{ cm}^2.[/tex]
Por outro lado, a embalagem B é um cilindro. As bases são círculos, e cada uma tem área [tex]\pi \times 4^2=16\pi \text{ cm}^2.[/tex] Já a face lateral do cilindro é um retângulo de altura [tex]20 \text{ cm}[/tex] e largura equivalente ao comprimento da circunferência da base: [tex]2\pi \times 4=8\pi[/tex]. Assim, a área superficial da embalagem B é dada por
[tex]\qquad B=(2\times 16\pi)+(20\times 8\pi)=192\pi\approx 603\text{ cm}^2.[/tex]
Logo, a embalagem B é mais econômica, e a diferença entre seu custo e o custo da embalagem A é de aproximadamente
[tex]\qquad (656-603)\times 0,1=R\$\, 5,30[/tex].
Solução elaborada pelos Moderadores do Blog.
