Nesse contexto, a Modelagem Matemática é um processo que envolve a representação de situações do mundo real por meio de conceitos matemáticos, com o objetivo de analisar, compreender e prever o comportamento dessas situações. De um lado, têm-se os dados e as intuições fornecidos pelo problema real; de outro, constrói-se um modelo — uma tentativa de descrever a realidade por meio de leis matemáticas. Esse modelo, após ser analisado e estudado com ferramentas matemáticas e computacionais, precisa ser confrontado com dados reais para sua validação. Assim, na modelagem, teoria matemática e realidade se retroalimentam de forma contínua.
Modelos Matemáticos: Exemplos Iniciais
Talvez você não perceba, mas modelos matemáticos estão sempre presentes em nosso cotidiano. Vamos ver alguns exemplos?
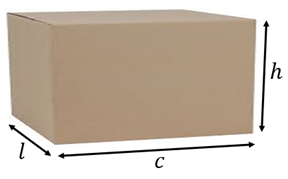
Para essa situação, o modelo matemático que nos fornece o volume interno da caixa é bem simples:
[tex] \text{Volume} = c \times l \times h[/tex].
O modelo é preciso? Bem, em nosso exemplo, não pensamos na espessura do papelão, na exatidão dos ângulos e das medidas e em outras coisas do “mundo real”. Mas, o modelo é bom o suficiente para ser útil! Por exemplo, o cálculo do volume de reservatórios de água, como cisternas ou caixas d’água, é essencial para garantir o abastecimento adequado e evitar desperdícios. Outro exemplo importante é o de calcular a capacidade de armazenamento, ainda que aproximada, em meios de transporte ou armazéns.
Havendo maior necessidade de precisão, detalhes como a espessura do papelão e a exatidão das medidas angulares serão importantes. Já dizia o estatístico britânico George Box que…

Vamos continuar com alguns exemplos.
Modelagem por Funções do Primeiro Grau
Primeiramente, vamos transformar litros em metros cúbicos. Sabemos que [tex]1000~l=1\, \text{ m}^3.[/tex] Logo, [tex]15~000~l=15\, \text{ m}^3,[/tex] ou seja, temos um excedente de [tex]5\, \text{ m}^3[/tex]. O valor a ser pago é calculado da seguinte forma:
[tex]\qquad \text{Valor a ser pago}=8 \times 5+40=R\$ ~80.[/tex]
O salário a ser recebido é calculado da seguinte forma:
[tex]\qquad \text{Salário}=10\% \times 13500+1800=0,1\times 13500+1800=R\$\, 3150.[/tex]
Você reparou que as duas situações foram modeladas por funções do tipo [tex]f(x)=ax+b[/tex]? No primeiro exemplo, a função [tex]f[/tex] determina o valor da conta a ser paga, sendo
[tex]\qquad x=\text{Excedente, em m}^3,\quad a=8 \text{ (taxa por cada m}^3\text{ excedente)},\quad b=40 \text{ (taxa fixa)}.[/tex]
Já no segundo exemplo, a função [tex]f[/tex] determina o salário mensal do vendedor, sendo
[tex]\qquad x=\text{Total das vendas, em reais},\quad a=0,1 \text{ (porcentagem de lucro)},\quad b=1800 \text{ (salário de segurança)}.[/tex]
Como vocês já devem conhecer, este tipo de função é chamado de Função Afim ou Função do Primeiro Grau. Embora seja um tipo simples de função, várias situações reais podem ser modeladas a partir de funções afins!
Modelagem por Funções do Segundo Grau
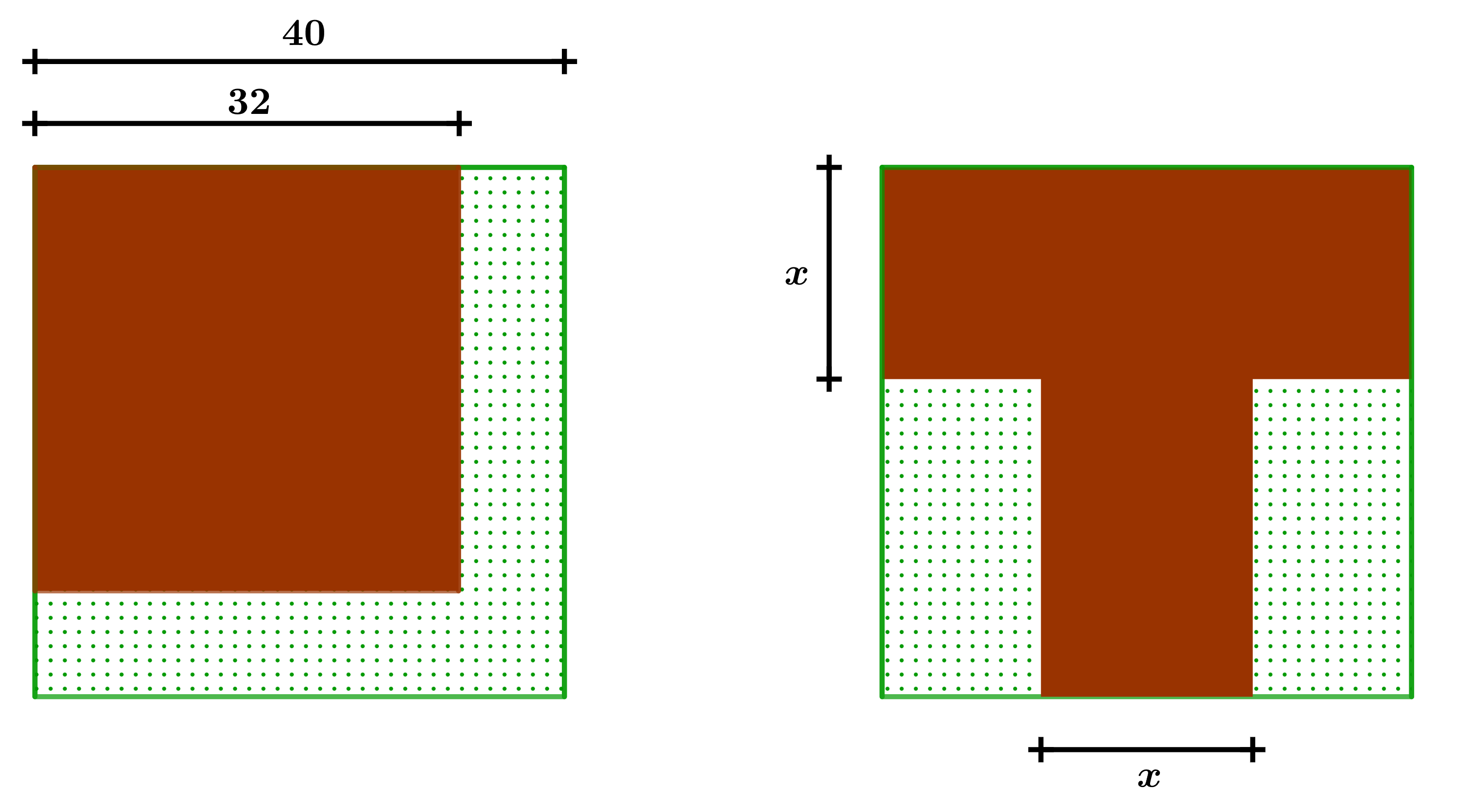
A função [tex]A[/tex] que fornece a área do armazém em T é dada por
[tex]\qquad A(x)=x\times 40+ x\times(40-x)=-x^2+80x.[/tex]
Queremos encontrar o valor de [tex]x[/tex] para o qual
[tex]\qquad A(x)=32^2=1024[/tex], ou seja,
[tex]\qquad -x^2+80x=1024[/tex], o que pode ser reescrito como
[tex]\qquad x^2-80x+1024=0.[/tex]
Solucionamos essa equação do segundo grau:
[tex]\qquad x=\dfrac{-(-80)\pm\sqrt{(-80)^2-4\times 1\times 1024}}{2\times 1},[/tex]
[tex]\qquad x=\dfrac{80\pm\sqrt{6400-4096}}{2},[/tex]
[tex]\qquad x=\dfrac{80\pm\sqrt{2304}}{2},[/tex]
[tex]\qquad x=\dfrac{80\pm48}{2},[/tex]
[tex]\qquad x_1=64, \quad x_2=16.[/tex]
Como, pelas dimensões do terreno, devemos ter [tex]x\lt40[/tex], obtemos a solução [tex]x=16\text{ m}[/tex].
Ao longo de um período de tempo observou-se que, se o preço das unidades variava, as vendas também variavam de acordo com a seguinte relação:
- a cada [tex]7[/tex] reais de aumento ou de desconto no preço de cada unidade, a venda diminuía ou aumentava em [tex]3[/tex] unidades, respectivamente.
A partir dessas observações, a que preço a receita seria máxima?
Na Sala de Atividades Voltando de um passeio pelo mundo da Equação Quadrática: Ideias e aplicações, as equações quadráticas são utilizadas para modelar diversos tipos de situações reais, tais como problemas de movimento, custo e receita, e problemas relativos ao estudo do espaço (atividades preparadas especialmente para futuros astronautas). Dêem uma passadinha por lá, confiram a solução do Exemplo 5 e muitos outros problemas interessantes!
Modelagem por Funções Exponenciais
Um exemplo um pouco mais sofisticado de modelo matemático é o do crescimento populacional de bactérias.
Vamos analisar a seguinte questão:
Vamos criar um modelo matemático para o crescimento dessa população de bactérias:
Suponha que o tempo [tex]x[/tex] esteja em minutos e seja [tex]T(x)[/tex] o total de bactérias por mililitro após o tempo [tex]x[/tex]. Como encontrar uma expressão para [tex]T(x)[/tex]?
Em primeiro lugar, quantas “meias horas” estão em [tex]x[/tex]? Como [tex]x[/tex] está em minutos, há [tex]x/30[/tex] “meias horas” em [tex]x[/tex]. A cada uma dessas “meias horas”, a população triplica.
Então, nosso modelo é dado por
[tex]\qquad T(x)= \text{quantidade inicial de bactérias}\times3^{\text{quantidade de “meias horas”}}=10\,000\times 3^{x/30}=10^4\cdot 3^{x/30}.[/tex]
Para responder a questão, como
[tex]\qquad T(x)= 2,43\cdot 10^6[/tex], então
[tex]\qquad 10^4\cdot 3^{x/30}=2,43\cdot 10^6[/tex], isto é,
[tex]\qquad 3^{x/30}=243[/tex].
Observe que [tex]243=3^5[/tex]. Logo, o problema se reduz à equação [tex]3^{x/30}=3^5[/tex]. Aplicando o logaritmo de base [tex]3[/tex], obtemos [tex]x/30=5[/tex], ou seja, [tex]x=150 [/tex] minutos (2 horas e 30 minutos).
O modelo apresentado no Exemplo 6 é útil? Sem dúvida! Mas será que ele é preciso? Talvez não tanto. Afinal, as bactérias não morrem? Elas se reproduzem de forma contínua ou em intervalos regulares? Será que ao formularmos nosso modelo deixamos de lado outras informações relevantes sobre o processo…?
Outro conceito fundamental nas ciências naturais, especialmente em Física e Química, é o de meia-vida. Em contextos farmacológicos, a meia-vida de um medicamento corresponde ao intervalo de tempo necessário para que a quantidade dessa substância no organismo seja reduzida à metade do valor inicial. Essa diminuição ocorre, principalmente, em decorrência dos processos de eliminação realizados pelo corpo e das reações químicas que as substâncias sofrem ao interagir com outras moléculas.
A meia-vida é um parâmetro essencial, por exemplo, para:
- determinar os intervalos entre as doses de um remédio,
- definir a dosagem correta,
- entender por quanto tempo o medicamento permanece ativo no corpo.
Vamos modelar a quantidade de determinado medicamento presente no organismo de uma pessoa ao longo do tempo, usando o conceito de meia-vida.
A fórmula que descreve essa situação é:
[tex]\qquad Q(x)=800\cdot \left(\dfrac{1}{2} \right)^{x}[/tex],
onde [tex]Q(x)[/tex] é a quantidade de medicamento (em [tex]\text{ mg}[/tex]) restante no organismo após [tex]x[/tex] meias-vidas.
Observe que o tempo de meia-vida é necessário apenas se quisermos converter o número de meias-vidas em tempo real (observe que [tex]x=t/80[/tex], se o tempo [tex]t[/tex] estiver em minutos). Para o modelo matemático em si, utilizamos apenas o número [tex]x[/tex] de meias-vidas decorridas.
Para uma explicação detalhada sobre a construção desse modelo, acesse a Sala de Estudos sobre a Função Exponencial – Sala Introdutória.
O modelo do Exemplo 7 é preciso? Deve-se observar que esse parâmetro apresenta variações dependendo das características do indivíduo. Em geral, ele é fornecido para uma pessoa adulta com saúde regular. Além disso, nesse modelo, a quantidade da medicação no organismo vai se tornando cada vez menor, porém nunca zera completamente – o que não ocorre na vida real. Mas, com toda a certeza, o modelo é muito, muito útil!
Observe que a modelagem dessas duas últimas situações utilizam funções do tipo exponencial, ou seja, funções da forma [tex]f(x)=k \cdot a^x[/tex]. Enquanto as funções afins são úteis em contextos de crescimento ou decrescimento constante, como o cálculo de custos, conversão de unidades de medida e análise de movimentos uniformes, funções exponenciais nos ajudam a entender outros diversos fenômenos, como aqueles de crescimento ou decaimento acelerado.
Modelagem por Funções Logarítmicas
Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre [tex]E_1[/tex] e [tex]E_2[/tex]?
Confiram a solução desta questão e mais problemas de modelagem de terremotos com funções logarítmicas na Sala de Estudo: Logaritmos X Terremotos!
Nessa fórmula, [tex]C[/tex] é uma constante que depende da energia da bomba X. Sabendo-se que, [tex]1[/tex] minuto após a explosão de uma bomba X de [tex]1[/tex] megaton de energia, o cogumelo de fumaça tem altura de [tex]6[/tex] km, determine a altura do cogumelo de fumaça desta bomba [tex]3[/tex] minutos após a explosão.
Confira a solução AQUI.
Modelagem por Funções Trigonométricas
Qualquer movimento que se repete em um período de tempo fixo é considerado movimento periódico e pode ser modelado por funções senoidais ou cossenoidais. A amplitude de uma função senoidal ou cossenoidal é a distância da linha média ao valor máximo, ou da linha média ao valor mínimo. A linha média é o valor médio. Funções senoidais oscilam acima e abaixo da linha média, são periódicas e repetem valores em ciclos definidos. Observe pelos gráficos das funções seno e cosseno que o período de ambas as funções é [tex]2\pi[/tex], e a amplitude é [tex]1[/tex]:
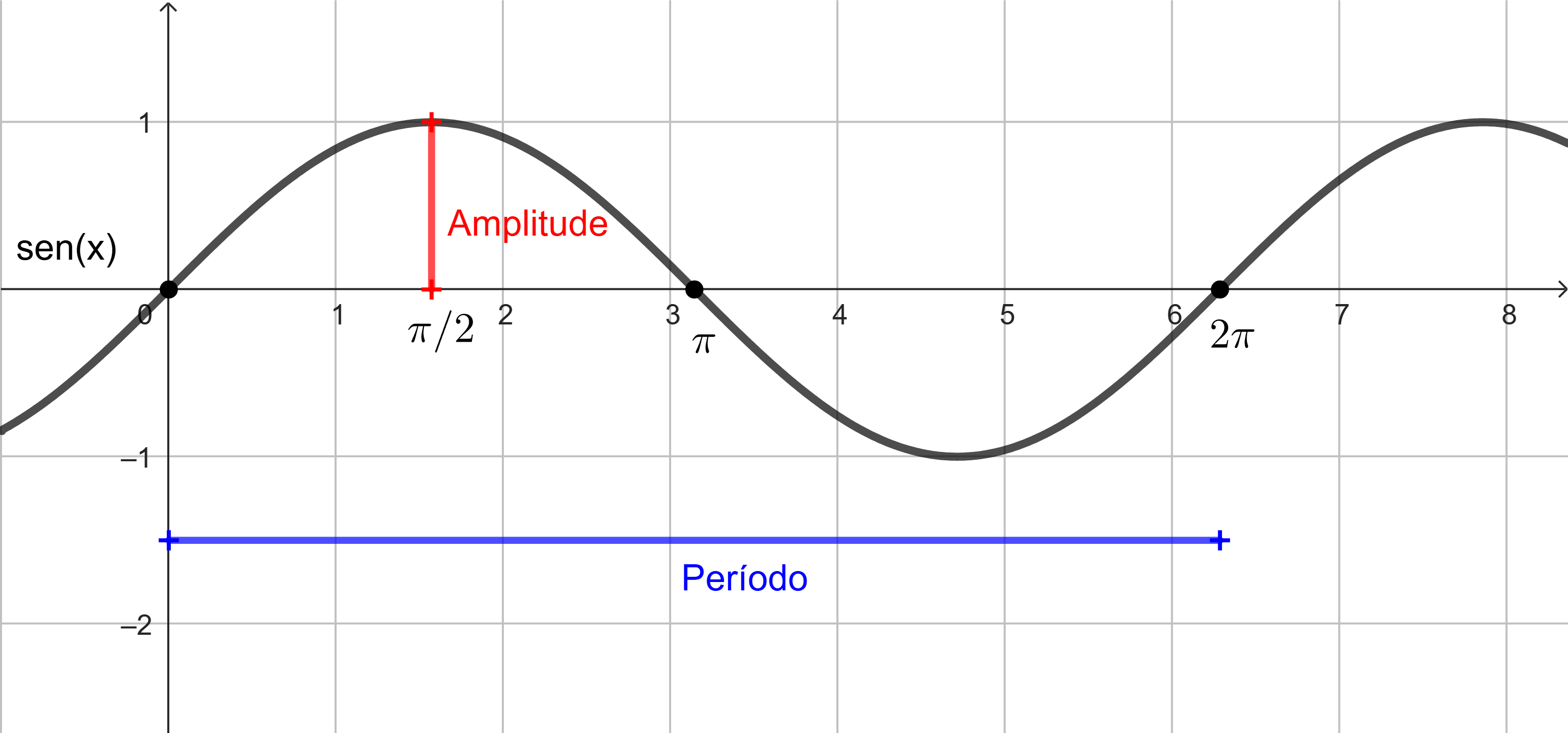
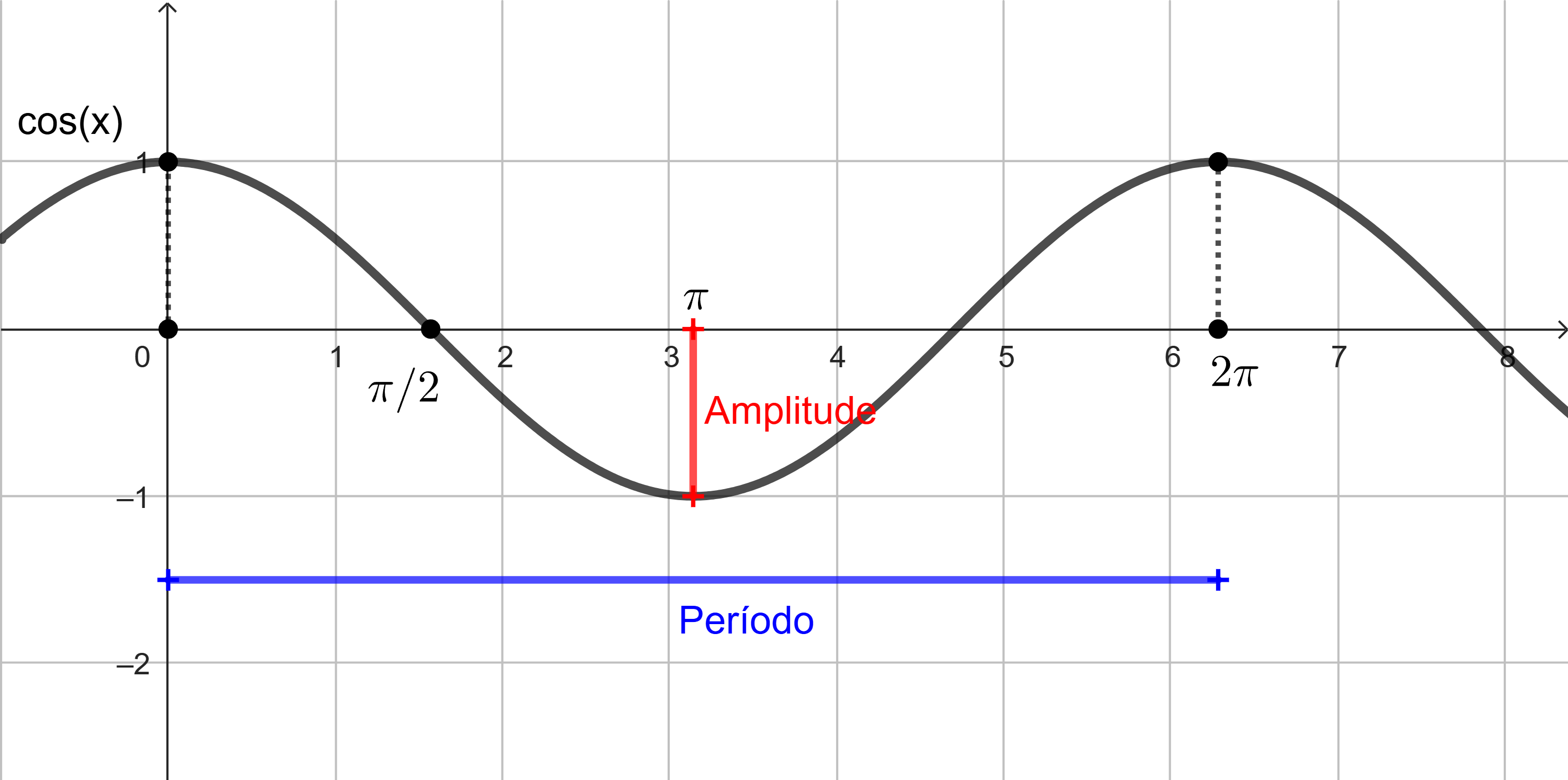
Assim,
[tex]\qquad \text{sen}(x\pm 2\pi k)=\text{sen}(x),[/tex]
[tex]\qquad \text{cos}(x\pm 2\pi k)=\text{cos}(x),[/tex]
para qualquer número inteiro [tex]k[/tex].
As formas gerais de uma função senoidal ou cossenoidal são dadas por
[tex]\qquad f(x) = A\text{sen}(Bx−C) + D[/tex]
ou
[tex]\qquad f(x) = A\text{cos}(Bx−C) + D,[/tex]
onde [tex]|A|[/tex] é a amplitude, [tex]B[/tex] está relacionado ao período, de modo que o período é [tex]2\pi/|B|[/tex], [tex]C[/tex] é o deslocamento horizontal e [tex]D[/tex] representa o deslocamento vertical em relação ao gráfico original. Observe que uma função cossenoidal pode ser vista como uma função senoidal deslocada horizontalmente, e vice-versa.
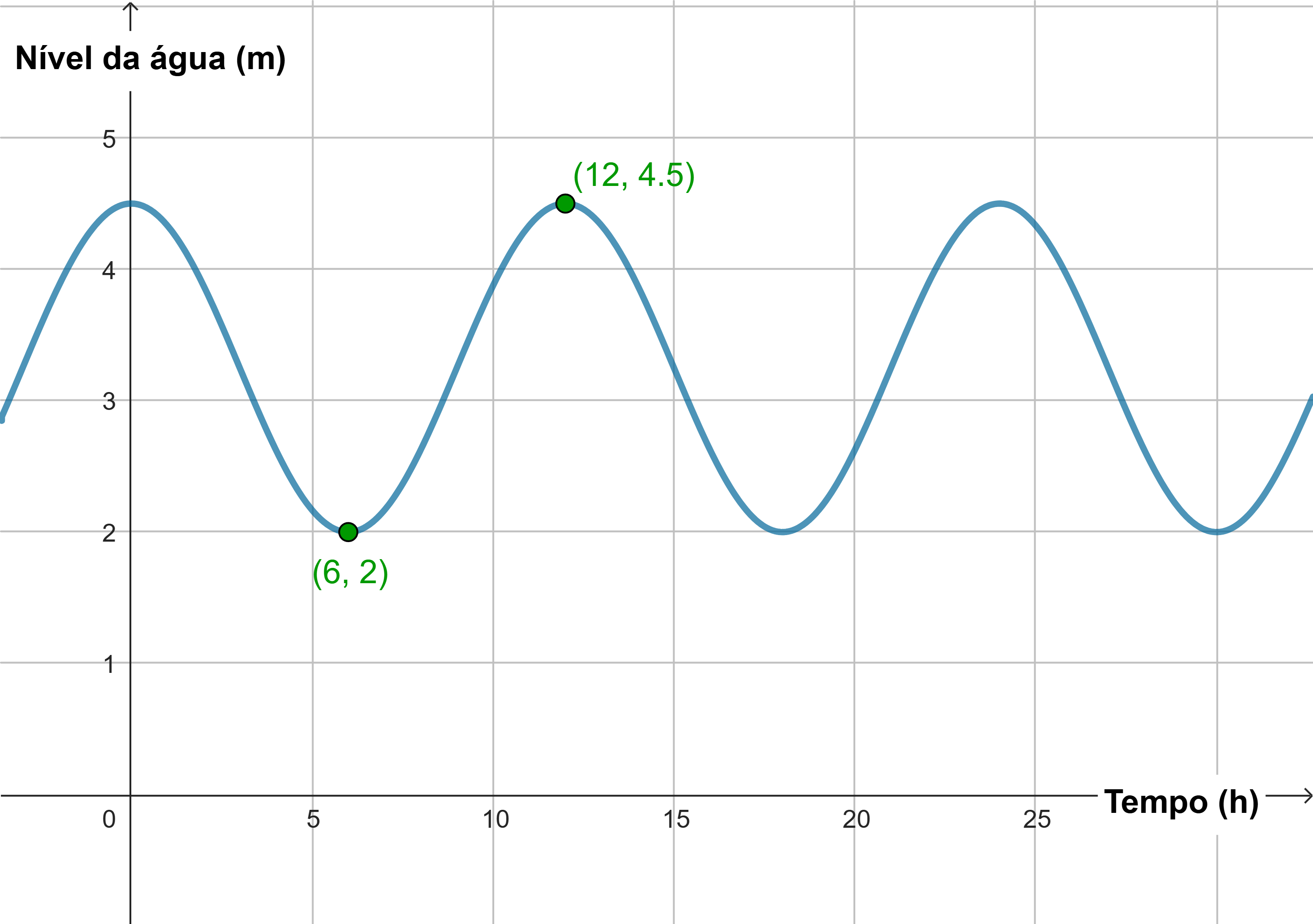
Como o nível de água varia de [tex]2[/tex] a [tex]4,5[/tex] metros, podemos calcular a amplitude como
[tex]\qquad |A|=\mid\frac{4,5-2}{2}\mid=1,25.[/tex]
O ciclo se repete a cada [tex]12[/tex] horas. Portanto, [tex]B[/tex] é tal que [tex]2\pi/B=12,[/tex] ou seja, [tex]B=\pi/6.[/tex]
Com amplitude [tex]1,25[/tex], o valor mínimo da função seria [tex]-1,25[/tex] se não usássemos uma translação vertical. Queremos que o valor mínimo seja [tex]2[/tex]. Logo, será necessária uma translação vertical [tex]D=3,25[/tex].
Como o ciclo se repete a cada [tex]12[/tex] horas, a função atinge seu máximo em [tex]t=0[/tex]. Usaremos a função cosseno, com valor positivo para [tex]A[/tex].
Assim, um modelo para a altura da maré nesta cidade em função do tempo, em horas, decorrido a partir da meia-noite, é dado por [tex]f(t)=1,25\cos(\pi t/6)+3,25.[/tex]
A função a seguir representa o preço, em reais, de um quilo dessa fruta, em função do tempo, expresso em meses. Aqui, [tex]t = 0[/tex] corresponde ao mês de janeiro:
[tex]\qquad P(t)=38 – 2 \cdot \cos \left[ \dfrac{\pi (t-1)}{6} \right].[/tex]
Em qual mês o preço da fruta atinge seu valor máximo?
Consulte a solução desta questão AQUI.
Agora é sua vez de tentar construir um modelo!
Introdução à Modelagem Epidemiológica
Uma das primeiras grandes contribuições da Matemática à Epidemiologia foi feita no século XVIII por Daniel Bernoulli (1700 – 1782). Os Bernoulli são a família mais extraordinária da história da ciência, tendo produzido nada menos que oito matemáticos de primeira linha. Eram suíços, mas Daniel nasceu na Holanda e viveu em vários países europeus. O pai, Johann, era professor de matemática, mas queria uma carreira mais rentável para o filho: obrigou-o a estudar negócios e medicina. Daniel aceitou, com a condição de que o pai lhe desse aulas particulares de matemática. Ficou muitíssimo bem equipado para contribuir para a erradicação da varíola da Europa.
[…]
Daniel Bernoulli desenvolveu um modelo matemático da doença […] para avaliar se seria vantajoso inocular todos os recém-nascidos dessa forma, visando prevenir o desenvolvimento posterior da doença. Utilizando os melhores dados disponíveis na época, ele concluiu que o ganho em vidas resultante da imunização proporcionada pela variolação generalizada seria muito superior às eventuais perdas causadas.
Marcelo Viana, abril de 2020, A Matemática e a erradicação de doenças.
Nesta sala, vamos aprender uma versão simplificada de um dos modelos epidemiológicos mais famosos e mais utilizados: o modelo SIR.
Em 1927, o modelo SIR (Suscetíveis-Infecciosos-Removidos) foi introduzido de maneira notável em um trabalho proposto por Kermack e McKendrick. Os autores concluíram que, ainda que o agente causador não perca sua infectividade e a população não seja inteiramente infectada, a análise de uma epidemia pode resultar de uma relação especial entre a densidade populacional, a infectividade e a taxa de recuperação.

Willian O. Kermack e Anderson G. McKendrick
O modelo SIR descreve a dinâmica de uma doença infecciosa (como a gripe), que se propaga numa certa população. A população é dividida em [tex]3[/tex] estados (compartimentos), [tex]S[/tex], [tex]I[/tex] e [tex]R[/tex], que variam de acordo com o tempo [tex]t[/tex]:
[tex]\qquad \bullet[/tex] Suscetíveis [tex]S[/tex]: são vulneráveis, podem pegar a infecção, mas atualmente não estão infectados;
[tex]\qquad \bullet[/tex] Infecciosos [tex]I[/tex]: atualmente infectados, que também podem infectar a outros;
[tex]\qquad \bullet[/tex] Removidos [tex]R[/tex]: indíviduos que já foram infectados e não são, atualmente, suscetíveis a uma reinfecção, porque se recuperaram e conseguiram imunidade (pelo menos durante o período em análise) ou porque faleceram.
A quantidade de indivíduos em cada compartimento no tempo [tex]n[/tex] é dada pelas funções [tex]S(n), I(n)[/tex] e [tex]R(n)[/tex], respectivamente.
Consideramos as seguintes hipóteses para simplificar a modelagem:
[tex]\qquad \bullet[/tex] A população [tex] N=S(n)+I(n)+R(n)[/tex] é constante, isto é, não consideramos nascimentos, mortes por outros fatores, migrações etc. Se estivermos interessados em um intervalo de tempo relativamente curto, essa hipótese é bastante razoável.
[tex]\qquad \bullet[/tex] Os recuperados da doença se tornam imunes a ela, pelo menos durante o período analisado.
[tex]\qquad \bullet[/tex] Assumimos que a população é homogeneamente misturada, isto é, os infecciosos e os susceptíveis estão distribuídos aleatoriamente na área em que a população vive. Esta hipótese nem sempre é correta, mas é útil para um modelo preliminar.
[tex]\qquad \bullet[/tex] Um susceptível fica infeccioso logo após a transmissão.
Consideramos o tempo em dias: dia 1, dia 2, dia 3, …, dia n. Assim, nosso modelo é discreto, isto é, a variação não é contínua, mas ocorre em momentos isolados (os dias).
Construindo o modelo
Consideramos dois dias consecutivos, o dia n e o dia n+1, e representamos por [tex]\Delta S[/tex], [tex]\Delta I[/tex] e [tex]\Delta R[/tex] as variações dos compartimentos [tex]S[/tex], [tex]I[/tex] e [tex]R[/tex] na passagem do dia n para o dia n+1, ou seja,
[tex]\qquad \Delta S = S(n+1) – S(n) = \text{Variação do número de suscetíveis};[/tex]
[tex]\qquad \Delta I = I(n+1) – I(n) = \text{Variação do número de infectados};[/tex]
[tex]\qquad \Delta R = R(n+1) – R(n) = \text{Variação do número de removidos};[/tex]
Como a única possibilidade de uma pessoa sair do compartimento [tex]S[/tex] é se for infectada e a única possibilidade de uma pessoa sair do [tex]I[/tex] é se for removida, temos
[tex](*)\begin{cases}\Delta S = -\text{Número de suscetíveis infectados do dia n para o dia n+1},\\ \Delta I = \text{Número de suscetíveis que foram infectados do dia n para o dia n+1} \\ \qquad\qquad- \text{Número de infectados que foram removidos do dia n para o dia n+1},\\
\Delta R = \text{Número de infectados que foram removidos do dia n para o dia n+1}.\end{cases}[/tex]
Vamos supor que o número de infectados que foram removidos do dia n para o dia n+1 é proporcional à quantidade de infectados no dia n. Por exemplo, podemos supor que, a cada dia, [tex]5\%[/tex] dos infectados são removidos (por recuperação ou falecimento). Podemos, portanto, assumir que existe uma taxa de remoção [tex]\gamma[/tex] do compartimento [tex]I[/tex], ou seja,
[tex]\qquad (i)\quad\text{Número de infectados que foram removidos do dia n para o dia n+1} = \gamma I(n).[/tex]
O inverso de [tex]\gamma[/tex], ou seja, [tex]1/\gamma[/tex], indica o tempo médio que um indivíduo permanece no compartimento infeccioso — o período durante o qual ele é capaz de transmitir a doença.
No caso da gripe comum, esse tempo é de aproximadamente [tex]5[/tex] dias. Isso significa que a taxa de recuperação, seu inverso, é de cerca de [tex]\gamma = 1/5[/tex] por dia, por indivíduo. Em outras palavras, a cada dia, em média, [tex]1/5[/tex] (ou [tex]20\%[/tex]) dos indivíduos infectados se recuperam e passam para o compartimento [tex]R[/tex], deixando de transmitir a doença.
Agora, para calcular o número de suscetíveis infectados do dia n para o dia n+1, podemos pensar da seguinte forma: a doença se propaga por contágio, algum tipo de contato entre um suscetível e um infeccioso. Suponhamos que cada indivíduo tem contato, em média, com [tex]c[/tex] pessoas por dia. Esta quantidade [tex]c[/tex] é a taxa de contato (“por indivíduo e por dia”). A doença é transmitida apenas quando uma pessoa infecciosa entra em contato com um suscetível. Mas, não há [tex]100\%[/tex] de certeza de que o contato resultará em contágio. Há uma probabilidade, digamos, [tex]p[/tex], de que um contato resulte em contágio.
Observe que:
- Se a população total é constituída por [tex]N[/tex] pessoas e é homogeneamente distribuída, a probabilidade de que um contato qualquer, no dia n, seja com um suscetível, é igual a [tex]S(n)/N[/tex].
- Portanto, uma pessoa infeciosa tem, em média, contato com [tex]cS(n)/N[/tex] suscetíveis por dia.
- Se [tex]p[/tex] é a probabilidade de que um contato resulte em contágio, uma vez que existem [tex]I(n)[/tex] indivíduos infectados no total, isso significa que o número de novas infecções, durante aquele dia, é [tex] cpS(n)I(n)/N[/tex].
Vamos chamar [tex]\beta=cp[/tex] de coeficiente de transmissão (“por dia”). Podemos, assim, escrever
[tex]\qquad(ii)\quad\text{Número de suscetíveis que foram infectados do dia } n \text{ para o dia }n+1 = \dfrac{\beta S(n) I(n)}{N}.[/tex]
Substituindo [tex](i)[/tex] e [tex](ii)[/tex] em [tex](*)[/tex], obtemos as seguintes variações das quantidades de suscetíveis, infectados e recuperados:
[tex]\qquad \Delta S = -\dfrac{\beta S(n) I(n)}{N},[/tex]
[tex]\qquad\Delta I = \dfrac{\beta S(n) I(n)}{N} – \gamma I(n),[/tex]
[tex]\qquad\Delta R = \gamma I(n).[/tex]

Vamos utilizar as variações que encontramos para obter as quantidades [tex]S(n+1)[/tex], [tex]I(n+1)[/tex] e [tex]R(n+1)[/tex] em função das quantidades [tex]S(n)[/tex], [tex]I(n)[/tex] e [tex]R(n)[/tex] e das taxas que definimos. Observe:
[tex]\qquad \Delta S = S(n+1) – S(n) = -\dfrac{\beta S(n) I(n)}{N},[/tex]
[tex]\qquad\Delta I = I(n+1) – I(n) = \dfrac{\beta S(n) I(n)}{N} – \gamma I(n),[/tex]
[tex]\qquad\Delta R = R(n+1) – R(n) = \gamma I(n).[/tex]
Isolando as quantidades [tex]S(n+1)[/tex], [tex]I(n+1)[/tex] e [tex]R(n+1)[/tex] no lado esquerdo das igualdades, obtemos, finalmente, o modelo SIR:
[tex]\qquad S(n+1) = S(n) – \dfrac{\beta S(n) I(n)}{N},[/tex]
[tex]\qquad I(n+1) = I(n) + \dfrac{\beta S(n) I(n)}{N} – \gamma I(n),[/tex]
[tex]\qquad R(n+1) = R(n) + \gamma I(n).[/tex]
Claro, esta é uma versão bastante simplificada do modelo SIR. Em sua forma mais completa, o modelo não é discreto, mas sim contínuo. Sua formulação utiliza derivadas, um conteúdo geralmente abordado apenas no ensino superior. Além disso, versões mais avançadas do modelo permitem incluir diversos outros fatores, como o nascimento e morte de indivíduos (dinâmica vital), o efeito de memória, entre outros aspectos mais complexos.
Mesmo assim, essa versão básica já é suficiente para gerar resultados significativos e úteis. Vamos explorá-la na prática?
Modelando uma situação real
Na edição de 4 de março de 1978 do British Medical Journal, havia um relatório com estatísticas detalhadas de uma epidemia de gripe em um colégio interno para meninos com um total de [tex]763[/tex] meninos. Este caso local é geralmente um exemplo inicial conhecido no aprendizado de modelos epidemiológicos. Os dados originais estavam disponíveis apenas em uma figura com alguns dados adicionais no texto principal; portanto, os números exatos variam dependendo da fonte. No total, [tex]512[/tex] meninos ficaram doentes. Havia [tex]763[/tex] meninos na escola.
Considere os seguintes dados:
\begin{array}{|c|c|}
\hline
\text{Data} & \text{Meninos “de cama”}\\
\hline
22/01 & 3 \\
\hline
23/01 & 8 \\
\hline
24/01 & 26\\
\hline
25/01 & 76\\
\hline
26/01 & 225 \\
\hline
27/01 & 298\\
\hline
28/01 & 258 \\
\hline
29/01 & 233\\
\hline
30/01 & 189\\
\hline
31/01 & 128\\
\hline
01/02 & 68 \\
\hline
02/02 & 29\\
\hline
03/02 & 14 \\
\hline
04/02 & 4\\
\hline
\end{array}
O uso da Modelagem Matemática por meio de atividades investigativas possibilita a participação ativa no processo de construção e reconstrução do conhecimento, o que pode gerar uma aprendizagem significativa. E quem sabe? Talvez vocês se tornem futuros pesquisadores, aplicando seus conhecimentos matemáticos no combate a epidemias e doenças. Ao longo da história, epidemias e pandemias têm causado grandes transtornos à sociedade. Prever a evolução de um surto é essencial para mitigar seus efeitos, e a área da modelagem epidemiológica desempenha um papel central nesse processo. Esperamos que tenham gostado desta breve introdução à Modelagem Matemática – em especial, à modelagem epidemiológica!
 |
Esperamos que tenham gostado desta breve introdução à Modelagem Matemática – em especial, à modelagem epidemiológica! |
[1] BRAUER, F. et al. Mathematical Models in Population Biology and Epidemiology, 2012.
[2] GENTIL ICONOCLASTA. Desafio Matemático − (UMO), 2024.
[3] George E. P. Box. Citação disponível em: <https://www.azquotes.com/author/22390-George_E_P_Box>. Acesso em: 14 jul. 2025.
[4] Google Brasil. Dicas de verificação de fatos. Disponível em: <https://brasil.googleblog.com/2021/03/dicas-verificacao-fatos.html>. Acesso em: 14 jul. 2025.
[5] KERMACK, W. O.; MCKENDRICK, A. G. Contributions to the mathematical theory of epidemics–i. 1927. Bulletin of mathematical biology, v. 53, n. 1-2, p. 33–55, 1991.
[6] LEHNING, H. La propagation des Épidémies. Maths et Médecine, 2016.
[7] Math is Fun. Mathematical Models. Disponível em: <https://www.mathsisfun.com/algebra/mathematical-models.html>. Acesso em: 14 jul. 2025.
[8] MONTEIRO, N. Z. Aplicação do cálculo de ordem arbitrária à epidemiologia. 2021. Dissertação (Mestrado em Matemática) – Instituto de Ciências Exatas, Universidade Federal de Juiz de Fora, Juiz de Fora, 2021.
[9] MURRAY, J. D. Mathematical biology: I. An introduction. Springer Science & Business Media, 2007.
[10] North Carolina State University. SIR Model – Student Version (BSM data). Disponível em: <https://www4.stat.ncsu.edu/~bjreich/BSMdata/SIR_readme.html>. Acesso em: 14 jul. 2025.
[11] OpenStax. (n.d.). 7.6: Modeling with Trigonometric Equations (Precalculus 2e). In Precalculus (2e). LibreTexts. Acessado em 1 setembro de 2025, de math.libretexts.org.
[12] QUBES Hub. Epidemic Modeling – Student Version. PDF disponível em: <https://qubeshub.org/resources/489/download/6-1-S-Epidemic-StudentVersion.pdf>. Acesso em: 14 jul. 2025.
[13] SILVA, S. R. da. O uso da Modelagem Matemática no Ensino de Funçoes na Educaçao Básica. 2014. Disponível em: <https://www2.unifap.br/matematica/files/2017/07/O-USO-DA-MODELAGEM-MATEM%C3%81TICA-NO-ENSINO-DE-FUN%C3%87%C3%95ES-NA-EDUCA%C3%87%C3%83O-B%C3%81SICA.pdf>. Acesso em: 14 jul. 2025.
[14] TAVARES, J. N. Modelo SIR em Epidemiologia. Revista de Ciência Elementar, v. 5, n. 2, 2017.
[15] VIANA, M. A relação entre a matemática e a erradicação de doenças, Folha de S.Paulo, abril de 2020. Disponível em: <https://www1.folha.uol.com.br/colunas/marceloviana/2020/04/a-relacao-entre-a-matematica-e-a-erradicacao-de-doencas.shtml>. Acesso em: 14 jul. 2025.
[16] WHAT IS EPIDEMIOLOGIC MODELING? In: News‑Medical.net, 2 jul. 2022. Disponível em: <https://www.news-medical.net/health/What-is-Epidemiologic-Modeling.aspx?utm_source=chatgpt.com>. Acesso em: 14 jul. 2025.
[17] Wikipedia. Matemática aplicada. Disponível em: <https://pt.wikipedia.org/wiki/Matem%C3%A1tica_aplicada>. Acesso em: 14 jul. 2025.
[18] Wikipedia (em inglês). Mathematical model. Disponível em: <https://en.wikipedia.org/wiki/Mathematical_model>. Acesso em: 14 jul. 2025.
[19] Wikipedia. Notícia falsa. Disponível em: <https://pt.wikipedia.org/wiki/Not%C3%ADcia_falsa>. Acesso em: 14 jul. 2025.

