Problema
(Indicado a partir do 1º ano do E. M.)
Uma Árvore Pitagórica é uma figura plana construída por etapas. Na Etapa 1, ela começa com um quadrado de lado 1 cm. Na Etapa 2, constroem-se dois quadrados acima do quadrado da Etapa 1, de tal forma que a medida de seus lados seja igual à medida dos catetos do triângulo retângulo isósceles que possui hipotenusa igual ao lado do quadrado da Etapa 1. Na Etapa 3, aplica-se a Etapa 2 em cada um dos novos quadrados obtidos, e assim por diante. Ou seja, em cada nova etapa, aplica-se a etapa anterior em cada um dos novos quadrados obtidos. A figura a seguir exibe as quatro primeiras etapas da construção da Árvore Pitagórica.
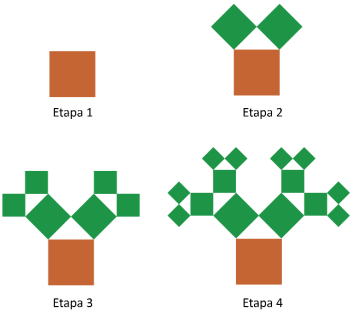
A partir de qual etapa da construção o lado de cada um dos novos quadrados obtidos fica, pela primeira vez, menor do que 1 décimo de milésimo do lado do quadrado da Etapa 1? Considere [tex]\log_{10} 2 = 0,3.[/tex]
Extraído de Fuvest 2024.
Solução
Note que, sendo [tex]L[/tex] a medida do lado do menor quadrado em uma etapa, e [tex]l[/tex] a medida do lado dos novos quadrados na etapa seguinte, temos, pelo Teorema de Pitágoras, que
[tex]\qquad l^2+l^2 = L^2\Rightarrow 2l^2=L^2\Rightarrow l^2=\dfrac{L^2}{2}\Rightarrow l=\sqrt{\dfrac{L^2}{2}}\Rightarrow l=\dfrac{L}{\sqrt{2}}\Rightarrow \boxed{l=\dfrac{L\sqrt{2}}{2}}.[/tex]
Sabemos que o lado do quadrado da etapa 1 mede 1 cm. Então, os lados dos novos quadrados a partir da etapa 1 são
[tex]\qquad 1, \dfrac{\sqrt{2}}{2}, \left(\dfrac{\sqrt{2}}{2}\right)^2, \left(\dfrac{\sqrt{2}}{2}\right)^3, \left(\dfrac{\sqrt{2}}{2}\right)^4, \cdots,[/tex]
que formam uma Progressão Geométrica [tex](a_n),[/tex] com primeiro termo igual a [tex]a_1= 1[/tex] e razão [tex]q = \dfrac{\sqrt{2}}{2}.[/tex]
Queremos saber qual é o valor de [tex]n[/tex] para o qual [tex]a_n\lt\dfrac{1}{10}\cdot \dfrac{1}{1000}\cdot a_1,[/tex] ou seja, [tex]a_n\lt\dfrac{1}{10~000}.[/tex]
Usando a fórmula do n-ésimo termo de uma PG, temos
[tex]\qquad a_n\lt\dfrac{1}{10~000}[/tex]
[tex]\qquad a_1\cdot q^{n-1}\lt\dfrac{1}{10^4}[/tex]
[tex]\qquad 1\cdot q^{n-1}\lt10^{-4}[/tex]
[tex]\qquad \left(\dfrac{\sqrt{2}}{2}\right)^{n-1}\lt10^{-4}[/tex]
[tex]\qquad \left(\dfrac{2^{\frac{1}{2}}}{2}\right)^{n-1}\lt10^{-4}[/tex]
[tex]\qquad \left(2^{-1/2}\right)^{n-1}\lt10^{-4}.[/tex]
Aplicando [tex]\log[/tex] em ambos os membros, ficamos com
[tex]\qquad \left(\log_{10} 2^{-1/2}\right)^{n-1}\lt\log_{10} 10^{-4}[/tex]
[tex]\qquad \log_{10} 2^{\frac{1-n}{2}}\lt-4[/tex]
[tex]\qquad \dfrac{1-n}{2}\log_{10} 2\lt-4[/tex]
[tex]\qquad \dfrac{1-n}{2}\cdot 0,3\lt-4[/tex]
[tex]\qquad \dfrac{1-n}{2}\lt-\dfrac{4}{0,3}[/tex]
[tex]\qquad 1-n\lt-\dfrac{8}{0,3}[/tex]
[tex]\qquad 1-n\lt-\dfrac{80}{3}[/tex]
[tex]\qquad n\gt\dfrac{80}{3}+1[/tex]
[tex]\qquad n\gt\dfrac{83}{3}[/tex]
[tex]\qquad n\gt\dfrac{83}{3}\approx 27,7.[/tex]
Logo, na 28ª etapa da construção o lado de cada um dos novos quadrados obtidos fica, pela primeira vez, menor do que 1 décimo de milésimo do lado do quadrado da etapa 1.
Solução elaborada pelos Moderadores do Blog.

