Problema
Um semicírculo, cujo centro está na hipotenusa de um triângulo retângulo, tangencia os outros dois lados desse triângulo, como é mostrado na figura a seguir.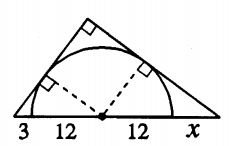
Se a hipotenusa está dividida em quatro segmentos de comprimentos [tex]3, 12, 12[/tex] e [tex]x[/tex], qual o valor de [tex]x[/tex]?
a) 2
b) 8
c) 3
d) 5
e) Nenhuma das respostas anteriores.
Solução
Observe que, com base na figura abaixo, os triângulos retângulos [tex]ADF[/tex] e [tex]FEC[/tex] são semelhantes ao triângulo retângulo [tex]ABC[/tex] e semelhantes entre si (Caso de semelhança A.A. (ângulo – ângulo)).
Além disso, utilizando as informações da figura do problema, podemos concluir que o raio do semicírculo é [tex]12[/tex].
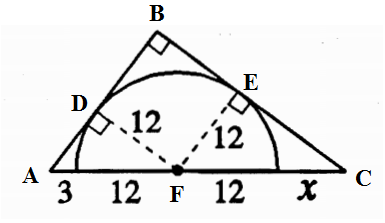
Note, também, que:
- Do triângulo [tex]ADF[/tex], sabemos que [tex]AF=15[/tex].
- Como [tex]DF=12[/tex], utilizando o Teorema de Pitágoras obtemos [tex]AD=9[/tex].
- Do triângulo [tex]FEC[/tex], sabemos que [tex]FE=12[/tex].
- Em razão da semelhança dos triângulos [tex]ADF[/tex] e [tex]FEC[/tex], temos que [tex]\dfrac{9}{12}=\dfrac{12}{EC}=\dfrac{15}{FC}[/tex]. Assim, [tex]CE=16[/tex] e [tex]FC=20[/tex].
Como [tex]FC=12+x[/tex], então [tex]\boxed{20=12+x}[/tex] e, portanto, [tex]\,\fcolorbox{black}{#eee0e5}{$x=8$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Fácil
 |
Se precisar, visite a nossa Sala Um pouco sobre semelhança de triângulos.
|
