Problema
(Indicado a partir do 1º ano do E. M.)
Na figura abaixo, [tex]ABCD[/tex] é um quadrilátero inscrito numa circunferência de centro em [tex]O[/tex]. As diagonais [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex] se intersectam perpendicularmente. Os comprimentos dos segmentos [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex] são, respectivamente, [tex]6\text{ cm}\,[/tex] e [tex]\,7\text{ cm}\,.[/tex]
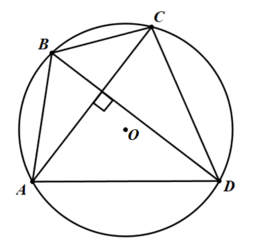
a) Quanto mede, em [tex]cm^2[/tex], a área do quadrilátero [tex]ABCD[/tex]?
b) Mostre que os triângulos [tex]AOB[/tex] e [tex]COD[/tex] possuem mesma área.
Extraído da Olimpíada Piauiense de Matemática – 2019.
Lembrete e Notações
✏ Se [tex]\alpha[/tex] e [tex]\beta[/tex] são duas medidas angulares tais que [tex]\alpha+\beta=180^{\circ}[/tex], então [tex]sen \; \alpha = sen \; \beta[/tex].
✏ Denotaremos a medida do ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]X\hat{V}Y[/tex].
✏ Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
Solução
a) Chame de [tex]P[/tex] a intersecção das diagonais do quadrilátero.
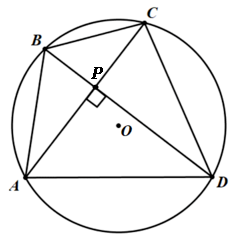
Assim, a medida da área do quadrilátero [tex]ABCD[/tex] é dada pela soma das medidas das áreas dos triângulos retângulos [tex]APB, BPC, CPD[/tex] e [tex]DPA[/tex]. Com isso, a medida [tex]S[/tex] da área de [tex]ABCD[/tex] é:
[tex]\,\,\\\
\qquad \begin{align*}
S&= \dfrac{AP\times BP}{2}+\dfrac{BP\times CP}{2}+\dfrac{CP\times DP}{2}+\dfrac{DP\times AP}{2}\\
&= \dfrac{BP\times (AP+CP)+DP\times (CP+AP)}{2}\\
&= \dfrac{(AP+CP)\times (BP+DP)}{2}\\
&= \dfrac{AC×BD}{2}\\
&= \dfrac{6\times7}{2}\\
&= 21\;cm^2.
\end{align*}[/tex]
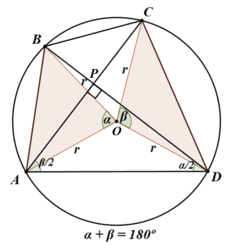
b) Seja [tex]r[/tex] o raio da circunferência circunscrita ao quadrilátero [tex]ABCD[/tex]. Então a área do triângulo [tex]AOB[/tex] é
[tex]\qquad\dfrac{1}{2}\cdot OA\cdot OB\cdot (sen \;A\hat{O}B) = \boxed{\dfrac{1}{2}\cdot r^2\cdot (sen \;A\hat{O}B)}[/tex]
e a área do triângulo [tex]COD[/tex] é
[tex]\qquad \dfrac{1}{2}\cdot OC\cdot OD\cdot (sen \;C\hat{O}D) =\boxed{\dfrac{1}{2}\cdot r^2\cdot (sen \;C\hat{O}D)}\,.[/tex]
Assim, para mostrarmos que estes dois triângulos têm mesma área, é suficiente mostrarmos que [tex]\,\fcolorbox{black}{#eee0e5}{$sen \;A\hat{O}B=sen \;C\hat{O}D$}\,.[/tex]
Pelo Teorema do Ângulo Central (visite esta sala), temos que:
[tex]\qquad A\hat{O}B = 2\;A\hat{D}B\;\;\;\textcolor{#800000}{(i)}\qquad [/tex] e [tex]\qquad C\hat{O}D = 2\;D\hat{A}C\;\;\;\textcolor{#800000}{(ii)}[/tex].
Veja, ainda, que
[tex]\qquad A\hat{D}B+D\hat{A}C = A\hat{D}P+D\hat{A}P = 90^{\circ}\;\;\;\;\textcolor{#800000}{(iii)}[/tex]
e, portanto, segue que:
[tex]\qquad \begin{align*}A\hat{O}B+C\hat{O}D &=2\;A\hat{D}B+2\;D\hat{A}C\hspace{8mm}\text{de}\; \textcolor{#800000}{(i)}\; \text{e}\; \textcolor{#800000}{(ii)}\\
&= 2(A\hat{D}B+D\hat{A}C)\\
&= 2\times 90^{\circ}\hspace{30mm}\text{de}\;\textcolor{#800000}{(iii)}\\
&=180^{\circ},
\end{align*}[/tex]
o que nos leva a concluir, pelo Lembrete, que [tex]\,\fcolorbox{black}{#eee0e5}{$sen \;A\hat{O}B=sen \;C\hat{O}D$}\,.[/tex]
Logo, os triângulos [tex]AOB[/tex] e [tex]COD[/tex] possuem mesma área.
Solução elaborada pelos Moderadores do Blog.
